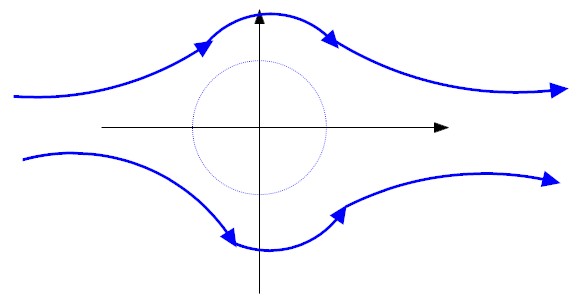
|
|
|
|
|
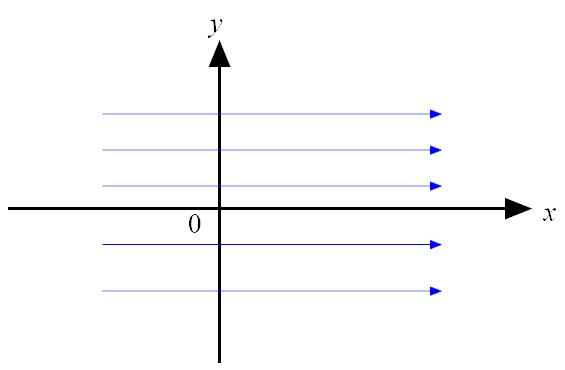 |
|
|
|
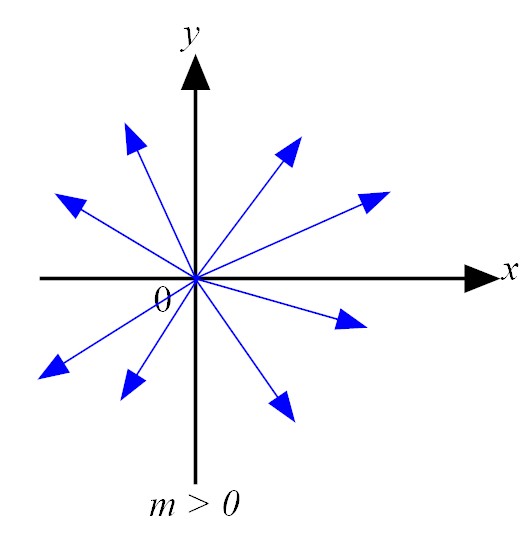 |
|
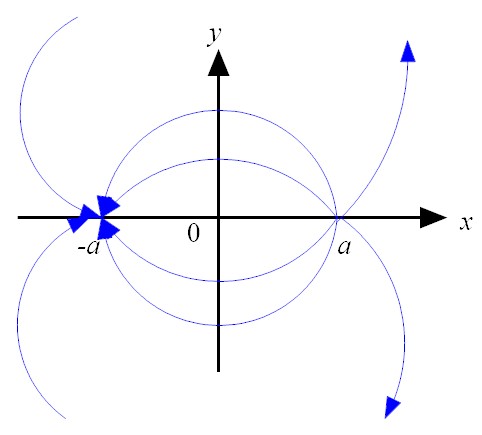 |
| (1) |
|
| (3) |
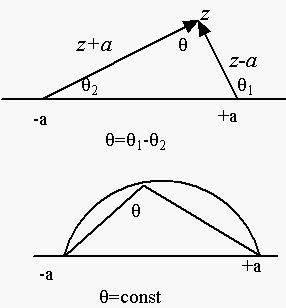 |
|
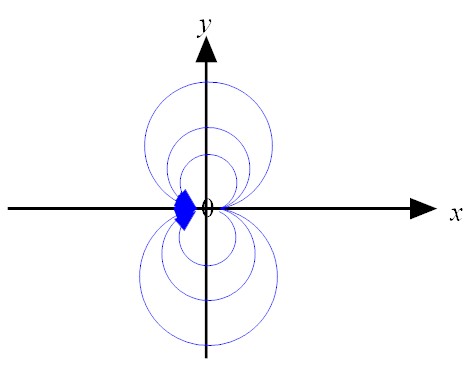 |
|
|
|
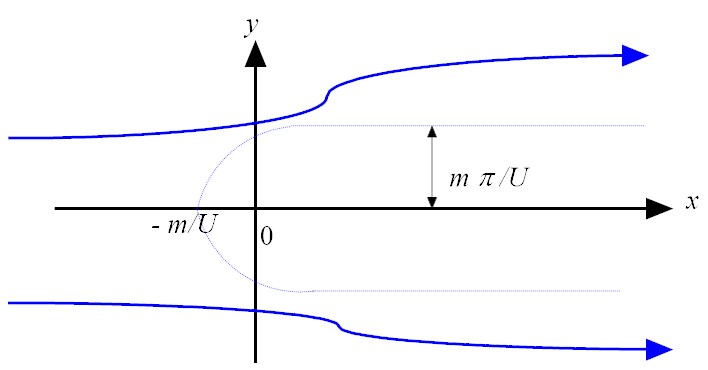
- c = 0 U r sin θ+ m θ = 0 can be satisfied for θ = 0 ( the positive x axis).
- c = m π
U r sin θ+ m θ = m π can be
satisfied for θ = π (the negative x axis). Besides this
trivial solution, one can also solve for r as
As θ→ π, r → m/U. Also as θ→ 0, r sin θ→ m π/U. For other values of θ, one can numerically compute r asr = m (π− θ) U sin θ. 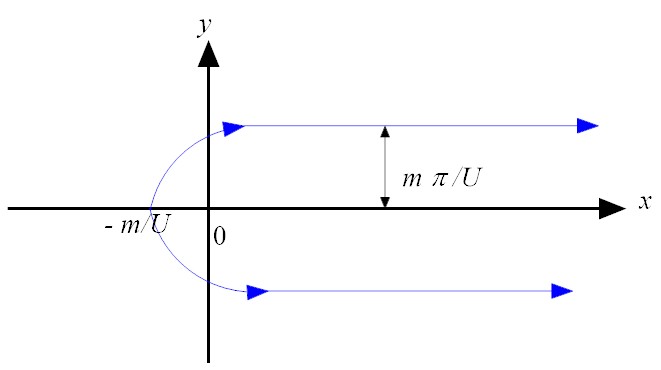
- For other values of c, the stream line should look like
 |
|
|
|
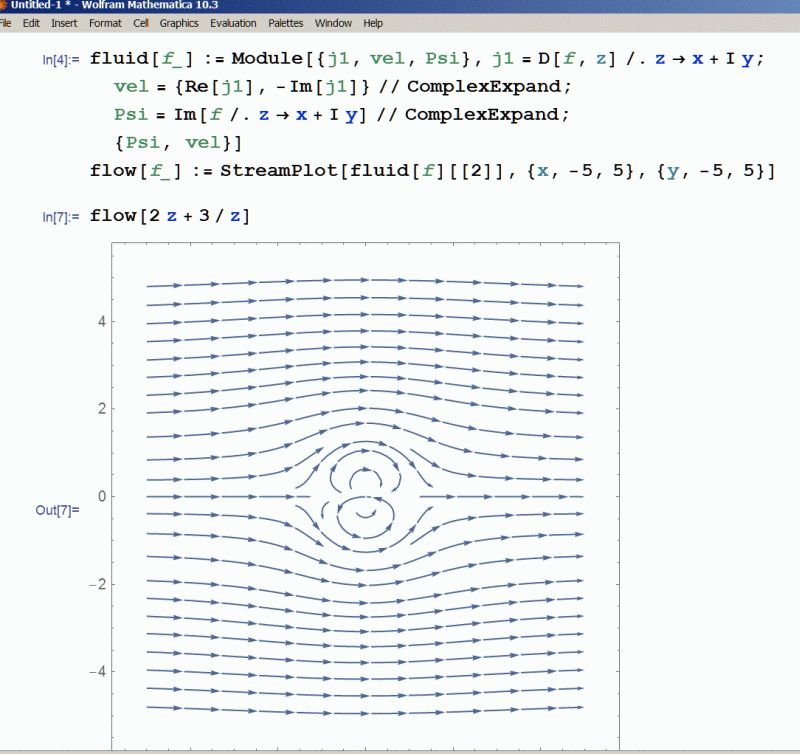
- c = 0
If sin θ = 0, it follows θ = 0, π. Otherwise,
U r − μ/r = 0 from which
This is a circle with μ/U as the radius.r = ⎛
√μ U. 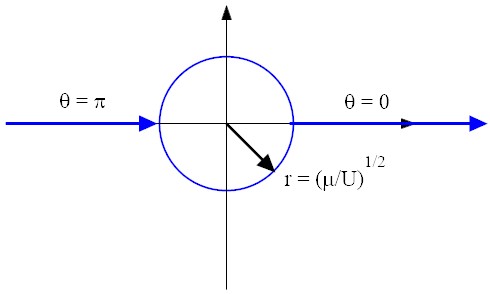
- For other values of c, the graph of (r, θ) may look like