ME5332 FINAL EXAMINATION

02:00-03:30PM, May 7, 2021

2

1. Find the fluid velocity components (u,v) for a complex potential function given as
   

   f(z) = z + i z .
2. Approximate e^x by d₁ + d₂ x over [0, 1] using the least square method.
3. Obtain the first two ON functions, (e₁, e₂), over [0, 2] by the Gram-Schmidt procedure for a₁ = 1 and a₂ = x where the inner product is defined as
   
   

   (f, g) = ⌠ ⌡ 2 0  x f(x) g(x) dx.
4. Using (e₁, e₂) in Problem 3, expand f(x)=x³ by a linear combination of e₁ and e₂ over [0, 2].
5. Find the eigenvalues and eigenfunctions for
   

   L en = λn en,     L ≡ − d2 dx2 ,

   
   

   en′(−1) = en(0)=0.
6. Solve
   

   −u"(x)=x,    u′(−1)=u(0)=0,

   using the eigenfunction expansion method and write down the first two terms.
7. Find a one-term approximate solution to the differential equation,
   

   L u = 1,     L ≡ d2 dx2 +x,     u(0) = u(1) = 0,

   (u"+x u=1) using the Galerkin method. Choose a base function which vanishes at x = 0, 1.
8. Using the Neumann series approach, compute A⁻¹ where
   

   A ≡ ⎛ ⎜ ⎜ ⎜ ⎝ 1 −1 1 0 1 1 0 0 1 ⎞ ⎟ ⎟ ⎟ ⎠ .
9. Solve the Laplace equation,
   

   ∂2 u ∂x2 + ∂2 u ∂y2 = 0,

   
   

   {(x,y),0 ≤ x ≤ 1, −∞ < y ≤ 0 }

   with the boundary condition shown by the eigenfunction expansion method.
10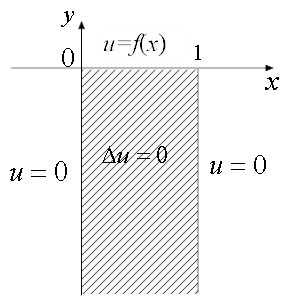. Rewrite
    

    −u"(x)+ ex u(x) = x,     u(0)=u(1)=0,

    in a weak form.

Solution

1.

u=1− 2 xy (x2+y2)2 ,     v = x2−y2 (x2+y2)2 .

2. Note that when the distance is minimized,

(ex − d1 − d2 x, 1)=0,    (ex − d1 − d2 x, x)=0,

so

− d1− d2 2 +e−1 = 0,     1 6 (−3 d1−2 d2+6)=0,

from which

d1 = 2 (2 e−5) ∼ 0.873127,     d2=6 (3−e)  ∼ 1.69031.

3.

e1 = a1 ||a1|| = 1 √2 .

e2′ = a2 − (a2, e1) e1 = x − (x, 1 √2 ) 1 √2 = x− 4 3 .

and

||e2′||2 = (e2′, e2′) = (x − 4 3 , x − 4 3 ) = 2 3 ,

so

e1 = 1 √2 ,     e2 = 3x − 4 2 .

*.

x3  ∼ c1 e1 + c2 e2,

c1 = (x3, e1)= 16√2 5  ∼ 4.52548,     c2=(x3, e2) = 16 5 .

5.

en(x) = √2 sin ⎛ ⎝ √   λn   x ⎞ ⎠ ,     λn = ⎛ ⎝ (n+ 1 2 )π ⎞ ⎠ 2   .

6.

xn = (x, en) = 4 √2 (−1)n (2 πn+π)2 .

~ u   = 32 sin ⎛ ⎝ πx 2 ⎞ ⎠ π4 − 32 sin ⎛ ⎝ 3 πx 2 ⎞ ⎠ 81 π4  ∼ 0.328511 sin ⎛ ⎝ πx 2 ⎞ ⎠ − 0.004055 sin ⎛ ⎝ 3 πx 2 ⎞ ⎠ .

Note: The exact solution is

u= 1 6 (3 x−x3).

Here is a comparison (no difference):

7. Choose e(x) = x (1−x). Then e′(x) = 1 − 2 x and e"(x) = −2.

L e = e"+ x e = −2 + x2 (1 − x),     (L e , e) = ⌠ ⌡ 1 0  (−2 + x2 −x3) x(1−x) dx = −19 60 .

(e, c) = ⌠ ⌡ 1 0  x (1−x) d x = 1 6 ,

so

−19 60 u1 = 1 6 ⇒ u1 = − 10 19 .

hence

~ u   = − 10 19 x(1−x)  ∼ − 0.526316x(1−x).

8.

A = ⎛ ⎜ ⎜ ⎜ ⎝ 1 −1 1 0 1 1 0 0 1 ⎞ ⎟ ⎟ ⎟ ⎠ = I + M     where M = ⎛ ⎜ ⎜ ⎜ ⎝ 0 −1 1 0 0 1 0 0 0 ⎞ ⎟ ⎟ ⎟ ⎠ .

Note

M2 = ⎛ ⎜ ⎜ ⎜ ⎝ 0 0 −1 0 0 0 0 0 0 ⎞ ⎟ ⎟ ⎟ ⎠    M3 = 0,

so

A−1 = (I + M)−1 = I − M + M2 = ⎛ ⎜ ⎜ ⎜ ⎝ 1 1 −2 0 1 −1 0 0 1 ⎞ ⎟ ⎟ ⎟ ⎠ .

9. Note that the eigenfunction and the eigenvalues are

en(x) = √2 sin  √   λn   x,     λn = (n π)2.

u(x, y) = ∑ (f, en) e√{λn} y en(x),

where

(f, en)= ⌠ ⌡ 1 0  f(x) en(x) dx.

10.

⌠ ⌡ 1 0  u′v′dx + ⌠ ⌡ 1 0  ex u v dx = ⌠ ⌡ 1 0  x v dx.