• Rectangular rule:
  
  

  I  ∼  h ×f0 + h ×f1 + h ×f2 + …+ h ×fn−1 = h ( f0 + f1 + …+ fn−1 ). (1)

  Example
  
  

  4 ⌠ ⌡ 1 0  1 1+x2 dx = 4 arctan x ⎢ ⎢ 1 0  = π.

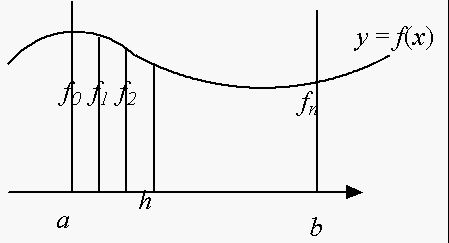
  1. C code

     /* Rectangular rule */ #include <stdio.h> double f(double x) {return 4.0/(1.0+x*x) ; } int main() { int i, n; double a=0.0, b=1.0, h, s=0.0 , x ; /* printf("Number of partitions = "); scanf("%d", &n) ; */ n=10; h = (b-a)/n ; for (i= 0;i<n;i++) s = s + f(a + i*h) ; s=s*h ; printf("Result =%20.12f\n", s) ; return 0; }

     Online C compiler
     Online C compiler(alternative)
     
     
     
  2. MATLAB (Octave) code

     f = @(x) 4/(1+x^2); a=0;b=1;s=0; n=10; %n=input('Enter n='); h=(b-a)/n; for i=0:1:n-1 s=s+f(a+i*h); end; s=s*h; fprintf('%f\n', s);

     Online Octave (Matlab)
• Trapezoidal rule:
  
  
  

  I  ∼  h 2 ( f0 + f1 ) + h 2 ( f1 + f2 )+ h 2 ( f2 + f3 )+ …+ h 2 ( fn−1 + fn ) = h 2 (f0 + 2 f1 + 2f2 +…+2fn−1+fn). (2)

  Implementation
  
  

  I  ∼  h 2 (f0+fn) + h ×(f1+f2+f3+…+ fn−1).

  1. C code

     /* Trapezoidal rule */ #include <stdio.h> double f(double x) {return 4.0/(1.0+x*x);} int main() { int i, n ; double a=0.0, b=1.0 , h, s=0.0, x; /* printf("Enter number of partitions = "); scanf("%d", &n) ; */ n=10; h = (b-a)/n ; for (i=1;i<=n-1;i++) s = s + f(a + i*h); s=h/2*(f(a)+f(b))+ h* s; printf("%20.12f\n", s) ; return 0; }

     Online C compiler
     Online C compiler(alternative)
  2. MATLAB (Octave) code

     f = @(x) 4/(1+x^2); a=0;b=1;s=0; n=10; %n=input('Enter n='); h=(b-a)/n; for i=1:1:n-1 s=s+f(a+i*h); end; s=h/2*(f(a)+f(b))+h*s; fprintf('%f\n', s);

     Online Octave (Matlab)
• Simpson's rule:
  
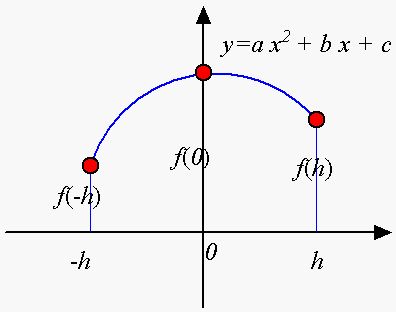  Approximate the curve that passes (−h, f(−h)), (0, f(0)) and (h, f(h)) by
  

  y = a x2+ b x + c.

  (3)

  
  

  f(−h) = a h2 − b h + c, (4) f(0) = c, (5) f(h) = a h2+ b h + c, (6)

  from which
  
  

  a = f(h)+ f(−h) − 2 f(0) 2h2 , (7) b = f(h)−f(−h) 2h , (8) c = f(0). (9)

  Hence,
  
  

  ⌠ ⌡ h −h  (a x2 + b x+ c) dx = ⌠ ⌡ h −h  ⎛ ⎝ f(h)+ f(−h) − 2 f(0) 2h2 x2 + f(h)−f(−h) 2h x+ f(0) ⎞ ⎠ dx = … = h 3 ⎛ ⎝ f(−h)+ 4 f(0)+ f(h) ⎞ ⎠ . (10)

  This is like a weighted average of f(−h), f(0) and f(h) as
  
  

  S ≈ f(−h)+ 4 f(0)+ f(h) 6 ×(2h).

  (11)

  By adding this for the interval [a,b], one obtains
  
  

  I  ∼  h 3 ⎛ ⎝ (f0 + 4f1 + f2 )+(f2 + 4f3 + f4 )+(f4 + 4f5 + f6 )+…+(f2n−2+ 4 f2n−1+f2n ) ⎞ ⎠  ∼  h 3 ⎛ ⎝ f0 +4 f1+2 f2 + 4f3 + 2f4 + …+ 2 f2n−2 + 4 f2n−1 + f2n ⎞ ⎠ , (12)

1. C code

   /* Simpson's rule */ #include <stdio.h> #include <math.h> double f(double x) {return 4.0/(1.0+x*x);} /* Note that the number of partitions is 2n, not n. */ int main() { int i, n ; double a=0.0, b=1.0 , h, s1=0.0, s2=0.0, s3=0.0, x; /* printf("Enter \"n\" (a half of the partitions) = "); scanf("%d", &n) ; */ n=5; h = (b-a)/(2.0*n) ; s1 = (f(a)+ f(b)); for (i=1; i<2*n; i=i+2) s2 = s2 + f(a + i*h); for (i=2; i<2*n; i=i+2) s3 = s3 + f(a + i*h); printf("The number of partitins is %d.\n", 2*n); printf("%20.12f\n", (h/3.0)*(s1+ 4.0*s2 + 2.0*s3)) ; return 0; }

   Online C compiler
   Online C compiler(alternative)
2. MATLAB (Octave) code

   f = @(x) 4/(1+x^2); a=0;b=1;s1=0; s2=0;s3=0; n=5; %n=input('Enter n= (must be even)'); h=(b-a)/(2*n); s1=(f(a)+f(b)); for i=1:2:2*n-1 s2=s2+f(a+i*h); end; for i=2:2:2*n-1 s3=s3+f(a+i*h) ; end; s= (h/3)*(s1+4*s2+2*s3); fprintf('%f\n', s);

   Online Octave (Matlab)

• Rectangular rule
  

  I  ∼ A + f′(ξ) h
• Trapezoidal rule
  

  I  ∼ A + f"(ξ) h2
• Simpson's rule
  

  I  ∼ A + f"′(ξ) h3

Computation of π