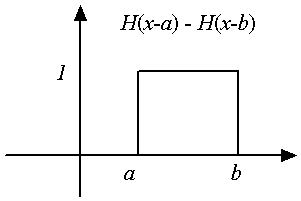| |
|
|
|
1
l
|
| ⌠
⌡
|
l
−l
|
p(x) cos |
n πx
l
|
dx |
| |
| |
|
|
| ⎡
⎣
|
1
l
|
p(x) |
l
nπ
|
sin |
n πx
l
| ⎤
⎦
|
l
−l
|
− |
1
l
|
| ⌠
⌡
|
l
−l
|
p′(x) |
l
nπ
|
sin |
nπx
l
|
dx |
| |
| |
|
|
0 + | ⎡
⎣
|
− |
1
nπ
|
p′(x) | ⎛
⎝
|
− |
l
nπ
|
cos |
nπx
l
| ⎞
⎠
| ⎤
⎦
|
l
−l
|
+ |
1
nπ
|
| ⌠
⌡
|
l
−l
|
p"(x) (− |
l
nπ
|
cos |
nπx
l
|
) dx |
| |
| |
|
|
|
2l
n2 π2
|
(−1)n p′(l) − | ⎡
⎣
|
l
n2 π2
|
p"(x) ( |
l
nπ
|
sin |
nπx
l
|
) | ⎤
⎦
|
l
−l
|
+ |
l
n2 π2
|
| ⌠
⌡
|
l
−l
|
p"′(x) |
l
nπ
|
sin |
n πx
l
|
dx |
| |
| |
|
|
|
2l
n2 π2
|
(−1)n p′(l) + | ⎡
⎣
|
l2
n3 π3
|
p"′(x) (− |
l
nπ
|
cos |
nπx
l
|
) | ⎤
⎦
|
l
−l
|
− |
l2
n3 π3
|
| ⌠
⌡
|
l
−l
|
p""(x) (− |
l
nπ
|
cos |
n πx
l
|
) dx |
| |
| |
|
|
|
2l
n2 π2
|
(−1)n p′(l)− |
2l3
n4 π4
|
p"′(l) + … |
| |
| |
|
|
2l
n2 π2
|
(−1)n | ⎛
⎝
|
p′(l)− |
l2
n2 π2
|
p"′(l)+… | ⎞
⎠
|
. |
| |
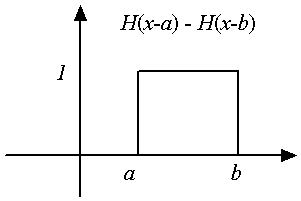
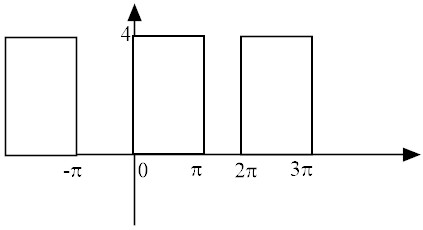 to show that
to show that