• HW page

• Template (Word file)

---

1. Derive the relationship between the backward difference operator, ~∆ f ≡ f(x) − f(x − h), and the differential operator, D f ≡ f′(x), and numerically obtain f′(1.0) from the table below using all the available information:


2.

f(x) ≡ ⎧ ⎪ ⎨ ⎪ ⎩ x 1 + exp(1/x)     (x ≠ 0) 0     (x = 0).

(a) Is f(x) continuous at x=0 ? State your rationale.
(b) Is f(x) differentiable at x=0 ? State your rationale.

HW 1 Solution

1.

~ ∆   f = f(x) − f(x − h) = f(x) − ⎛ ⎝ f(x) − h f′(x) + h2 2 f"(x) − … ⎞ ⎠ = ( 1 − e−h D) f.

Therefore,

~ ∆   = 1 − e−h D

(1)

or

D = − 1 h ln (1 − ~ ∆   ) = 1 h ⎛ ⎜ ⎝ ~ ∆   + ~ ∆   2   2 + ~ ∆   3   3 + ~ ∆   4   4 + … ⎞ ⎟ ⎠ .

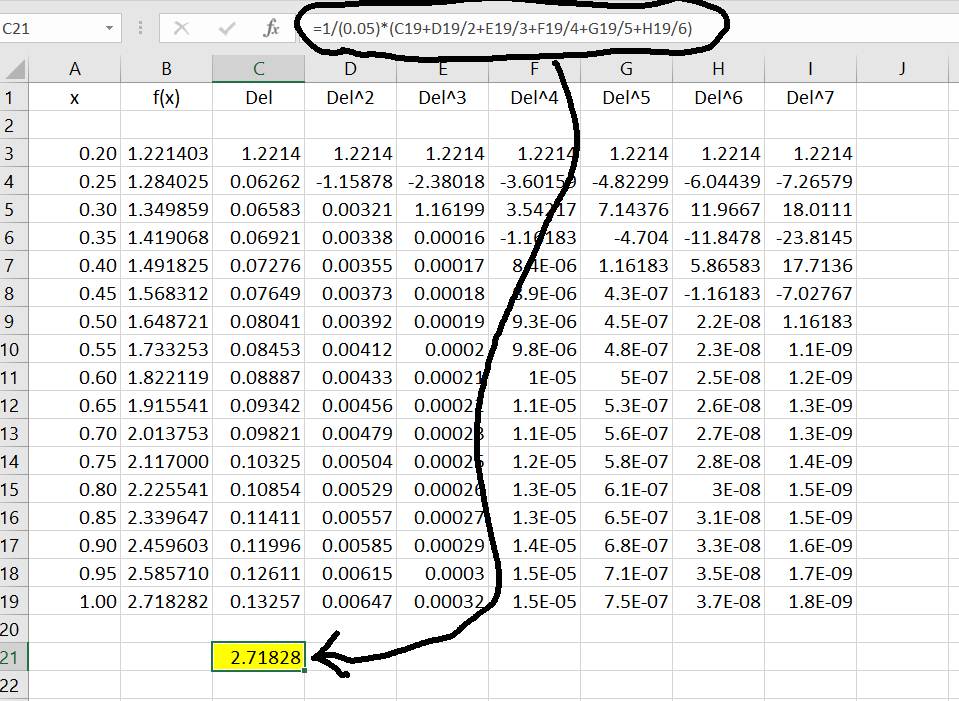
The values of f(x) is based on f(x) = e^x. Therefore, f′(1)=f(1)=2.71828. Your answer must match this value.

2. (a)

lim x → +0  x 1 + e1/x = 0, lim x → −0  x 1 + e1/x = 0

so

lim x → 0  f(x) = f(0),

hence, f(x) is continuous at x = 0. Note that

lim x→ +0  e1/x = ∞,        lim x→ −0  e1/x = 0.

(b)

f′(0) = lim h → 0  f(0 + h) − f(0) h = lim h → 0  1 1 + e1/h

but

lim h → +0  1 1 + e1/h = 0,        lim h → −0  1 1 + e1/h = 1,

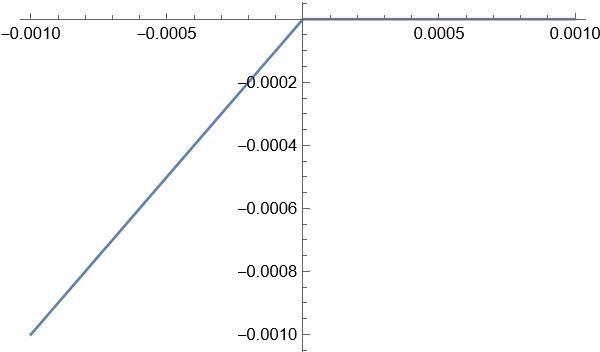
so f(x) is NOT differentiable at x = 0. Here is a graph of f(x) around x=0. It is seen that f(x) is continuous (no hole) but not differentiable (not smooth) at x=0.