 Laplace transform
Laplace transform
Example:
t^4 (must be lowercase t)
t



|
| (2) |
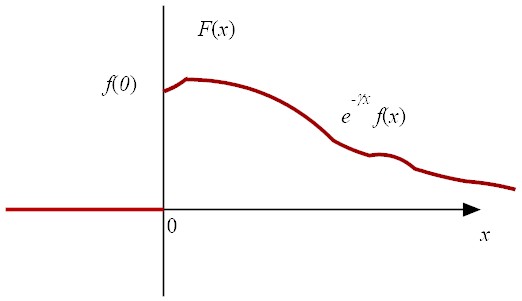 If we require that
If we require that
| (3) |
|
| (5) |
|
|
|
| (7) |
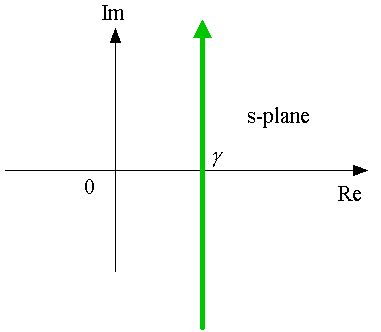 Equation (7) is called the Laplace transform of
f(x) and Eq. (6) is called the inverse Laplace transform.
As discussed in class, the Laplace transforms are special cases of the
Fourier transforms by restricting F(t)
2 to exp(−γt) f(t) for t > 0,
where γ is a positive number.
For the convergence of the Laplace transform, f(t) must be a function such that
e−γt f(t) → 0 as t→ ∞ for an appropriately chosen positive
value of γ. Such functions include
Equation (7) is called the Laplace transform of
f(x) and Eq. (6) is called the inverse Laplace transform.
As discussed in class, the Laplace transforms are special cases of the
Fourier transforms by restricting F(t)
2 to exp(−γt) f(t) for t > 0,
where γ is a positive number.
For the convergence of the Laplace transform, f(t) must be a function such that
e−γt f(t) → 0 as t→ ∞ for an appropriately chosen positive
value of γ. Such functions include
|
| (12) |
| (13) |
| (14) |
|
|
| (17) |
|
| (18) |
|
|
|
| (20) |
 Laplace transform
Laplace transform
Example: |
 Inverse Laplace transform
Inverse Laplace transform
Example: |
| (21) |
| (22) |
| (23) |
|
| (25) |
|
|
|
 Inverse Laplace transform
Inverse Laplace transform
|
| (32) |
| (33) |
| (34) |
| (35) |
| (36) |
| (37) |
|
| (40) |
|
| (42) |
|
| (44) |
|



|