#20 (11/10/2025)

Dirac delta functions and Heaviside step functions

Definition of Dirac delta function

The definition of the Dirac delta function is

⌠
⌡ 		∞

−∞ 
 δ(x) f(x) dx = f(0),
(1)
i.e. δ(x) is defined by its action as an operator and is therefore different from ordinary functions. The Dirac delta function is one of generalized functions (distributions, hyperfunctions) that are used in physics extensively.
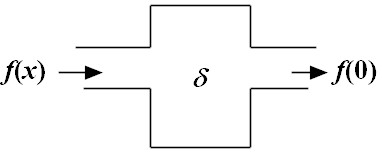
delta_1.jpg
The Dirac delta function can be realized by the limit of a sequence of functions defined as

wk(x) = ⎧
⎪
⎨
⎪
⎩
k
2
    |x| < 1
k
0
    otherwise
(2)
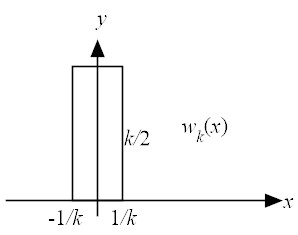
delta_2.jpg

⌠
⌡ 		∞

−∞ 
 wk(x) f(x) dx
=
⌠
⌡ 		1/k

−1/k 
 k
2
 f(x) dx
=
k
2
 ⌠
⌡ 		1/k

−1/k 
 f(x) dx
=
k
2
 ⌠
⌡ 		1/k

−1/k 
 ⎛
⎝ 		f(0)+ f′(0) x + f"(0)
2!
 x2 + f"′(0)
3!
 x3 + f""(0)
4!
 x4 + …⎞
⎠ 		dx
=
f(0) + f"(0)
6
 1
k2
 + f""(0)
120
 1
k4
 + …
 ∼ 
f(0)     as     k → ∞.
(3)
By comparing Eq. (1) with Eq. (3), one can obtain

δ(x) =
lim
k→ ∞ 
 wk(x).
(4)
In physics, a point force at x=a with a magnitude of F can be expressed as

w = F δ(x−a).
(5)

Derivatives of delta functions

It is also possible to define derivatives of delta functions as distributions. By using integrations by parts, one can start with

⌠
⌡ 		∞

−∞ 
 δ′(x) f(x) dx
=
[δ(x) f(x)]−∞∞− ⌠
⌡ 		∞

−∞ 
 δ(x) f′(x) dx
=
−f′(0).
(6)
So the action of δ′(x) is to (1) differentiate f(x), (2) evaluate f′(x) at x=0 and (3) multiply by (−1).
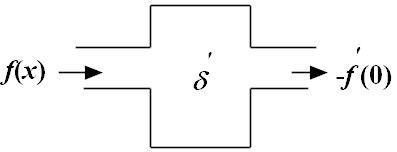
delta_3.jpg
To understand the physical meaning of δ′(x), consider a sequence of functions, mk(x), defined as

mk (x) ≡ ⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
4 k2
    − 1
2k
 < x < 0
− 4 k2
    0 < x < 1
2k
0
    otherwise.
(7)
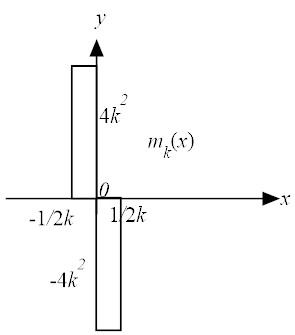
delta_4.jpg
Then,

⌠
⌡ 		∞

−∞ 
 mk(x) f(x) dx
=
⌠
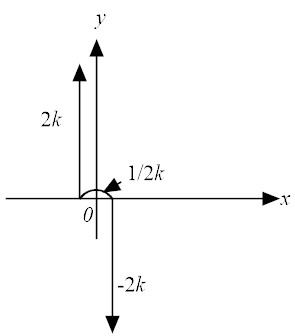
⌡ 		0

−1/(2k) 
 4 k2 f(x)dx +⌠
⌡ 		1/(2k)

0 
 (−4 k2) f(x)dx
=
4k2 ⌠
⌡ 		0

−1/(2k) 
 f(x)dx −4k2 ⌠
⌡ 		1/(2k)

0 
 f(x)dx
=
4k2 ⌠
⌡ 		0

−1/(2k) 
 ⎛
⎝ 		f(0)+ f′(0) x + f"(0)
2!
 x2 + f"′(0)
3!
 x3 + … ⎞
⎠ 		dx
−4 k2 ⌠
⌡ 		1/(2k)

0 
 ⎛
⎝ 		f(0)+ f′(0) x + f"(0)
2!
 x2 + f"′(0)
3!
 x3 + … ⎞
⎠ 		dx
=
4k2 ⎛
⎝ 		f(0)
2k
 − f′(0)
8 k2
 + f"(0)
48 k3
 − f"′(0)
384 k4
 +…⎞
⎠ 		−4k2 ⎛
⎝ 		f(0)
2k
 + f′(0)
8 k2
 + f"(0)
48 k3
 + f"′(0)
384 k4
 +…⎞
⎠
=
−f′(0) − f"′(0)
48
 1
k2
 − …
 ∼ 
−f′(0)     as     k→ ∞. 
(8)
By comparing Eq. (6) with Eq. (8), one finds
δ′(x) =
lim
k→ ∞ 
 mk(x).
(9)
If we replace the distributed load by the equivalent point force, the figure of mk(x) can be seen as a moment (couple) as
delta_5.jpg
It is thus seen that a point moment located at x=a with a magnitude of M1 can be expressed by δ′(x) as

M = M1 δ′(x−a).
(10)
Higher order derivatives of δ(x) can be evaluated in a similar manner. For instance, the second order derivative of δ(x), δ"(x), is

⌠
⌡ 		∞

−∞ 
 δ"(x) g(x) dx
=
⎡
⎣ 		δ′(x) g(x) − δ(x) g′(x)⎤
⎦ 		∞
−∞ 
 + ⌠
⌡ 		∞

−∞ 
 δ(x) g"(x) dx
=
g"(0),
(11)
in general
⌠
⌡ 		∞

−∞ 
 δ(n)(x) g(x) dx = (−1)n g(n)(0).
(12)

Heaviside step function

The Heaviside step function, H(x), is defined as

H(x) = ⎧
⎪
⎨
⎪
⎩
0
    x < 0
1
    x > 0.
(13)
delta_6.jpg
Obviously, H(x) is discontinuous at x=0 and in traditional calculus, the derivative of H(x) at x = 0 does not exist. However, consider

⌠
⌡ 		∞

−∞ 
 H ′(x) g(x)dx
=
⎡
⎣ 		H(x) g(x) ⎤
⎦ 		∞
−∞ 
 − ⌠
⌡ 		∞

−∞ 
 H(x) g′(x) dx
=
g(∞)−0 − ⌠
⌡ 		∞

0 
 g′(x) dx
=
g(∞) − ⎡
⎣ 		g(x)⎤
⎦ 		∞
0 
=
g(0).
(14)
where an integration by parts was used. By comparing Eq. (14) with Eq. (1), one can find

H ′(x) = δ(x).
(15)
which implies that if one includes δ(x) in a group of functions, it is possible to differentiate discontinuous functions as many times as needed.

Examples


    (1)
    g(x) δ(x) = g(0) δ(x).
    (Proof)
    ⌠
    ⌡     		∞

    −∞ 
    		 ⎛
    ⎝     		g(x) δ(x)⎞
    ⎠     		f(x) dx
    =
    ⌠
    ⌡     		∞

    −∞ 
    		 δ(x) ⎛
    ⎝     		g(x) f(x)⎞
    ⎠     		dx
    =
    g(0) f(0).
    		(16)
    On the other hand,

    ⌠
    ⌡     		∞

    −∞ 
    		 ⎛
    ⎝     		g(0) δ(x)⎞
    ⎠     		f(x) dx
    =
    ⌠
    ⌡     		∞

    −∞ 
    		 δ(x) ⎛
    ⎝     		g(0) f(x)⎞
    ⎠     		dx
    =
    g(0) f(0).
    		(17)

    (2)
    x δ′(x) = − δ(x).
    (Proof)
    ⌠
    ⌡     		∞

    −∞ 
    		 ⎛
    ⎝     		x δ′(x)⎞
    ⎠     		f(x) dx
    =
    ⌠
    ⌡     		∞

    −∞ 
    		 δ′(x) ⎛
    ⎝     		x f(x)⎞
    ⎠     		dx
    =
    − d
    dx
    		 (x f(x)) |x=0
    =
    − ( f(x)+ x f′(x))|x=0
    =
    − f(0).
    		(18)
    On the other hand,

    ⌠
    ⌡     		∞

    −∞ 
    		 ⎛
    ⎝     		−δ(x)⎞
    ⎠     		f(x) dx = − f(0).
    		(19)

    (3)

    x2 δ"(x) = 2 δ(x).
    (Proof) (skipped)
    (4)

    d4
    dx4
    		 |x|3 = 12 δ(x).
    (Proof) Shown in class.
    (5)
    d
    dx
    		 |x| = 2 H(x)−1.
    (Proof)
    Noting that

    |x| = x H(x) − x H(−x).
    		(20)
    (Explanation) If x > 0, H(−x)=0 and H(x)=1 so xH(x)=x. If x < 0, H(x)=0 and H(−x)=1 so −x H(−x)=−x.

    d
    dx
    		 |x|
    =
    H(x) + xδ(x) − H(−x) −(−1) x δ(−x)
    =
    2H(x)−1 + 2x δ(x),
    		(21)
    where

    H(−x) = 1− H(x),
    		(22)
    and the fact that δ(x)=δ(−x) was used.
    It should be noted that
    x δ(x) = 0,
    		(23)
    as
    ⌠
    ⌡     		∞

    −∞ 
    		 ⎛
    ⎝     		x δ(x)⎞
    ⎠     		g(x) dx
    =
    ⌠
    ⌡     		∞

    −∞ 
    		 δ(x) ⎛
    ⎝     		x g(x)⎞
    ⎠     		dx
    =
    xg(x)|x=0
    =
    0,
    		(24)
    so

    d
    dx
    		 |x| = 2H(x)−1.
    		(25)
    This conclusion can be also obtained geometrically (try!).

Integration of singularity functions


⌠
⌡ 		x

−∞ 
 δ(x−a) dx
=
H(x−a)
(26)
⌠
⌡ 		x

−∞ 
 H(x−a) dx
=
(x − a) H(x−a)
(27)
⌠
⌡ 		x

−∞ 
 (x−a) H(x−a) dx
=
(x−a)2
2
 H(x−a)
(28)
⌠
⌡ 		x

−∞ 
 (x−a)2 H(x−a) dx
=
(x−a)3
3
 H(x−a)
(29)
…
(30)
In general,
(x−a)n H(x−a) = ⎧
⎪
⎨
⎪
⎩
0
    x < a
(x−a)n
    x > a
(31)
i.e. the function, (x−a)n H(x−a), is identically 0 when the argument, x−a, is negative.

Beam loading

beam1.jpg
Example
beam2.jpg
A cantilevered beam is subject to a partially distributed load starting at x=a. The problem is to find the reaction force and the point moment at x=0.
First we can assume that all the unknown quantities, i.e. R1 and M1, are positive, i.e. the directions shown in the figure. Once we can express q(x) using the singularity functions, V(x) and M(x) can be automatically expressed by integrating each singular function as

q(x)
=
M1 δ′(x) + R1 δ(x) − w H(x−a),
(32)
V(x)
=
M1 δ(x) + R1 H(x) − w (x−a) H(x),
(33)
M(x)
=
M1 H(x) + R1 x H(x) − w (x−a)2
2
 H(x−a).
(34)
Substitute x=l+ϵ where ϵ is a small number, i.e. we are looking at a point a little bit right to the end of the beam. Since there is no beam material at x=l+ϵ, both M(x) and V(x) should be zero. So Eqs. (33, 34) become

0
=
M1 ×0 + R1 ×1 − w (l−a)
(35)
0
=
M1 ×1 + R1 ×l− w (l−a)2
2
(36)
Note that δ(x)|x→ l = 0 and H(x)|x→ l = 1 etc.... Eqs. (35, 36) can be solved to yield

R1
=
w (l−a)
(37)
M1
=
− w
2
 (l+a)(l−a)
(38)
The result of Eq. (38) implies that the correct sign of M1 is ccw. It is noted that Eq. (35) is the balance-of-force equation while Eq. (36) is the balance-of-moment equation


File translated from TEX by TTH, version 4.03.
On 09 Nov 2025, 19:31.