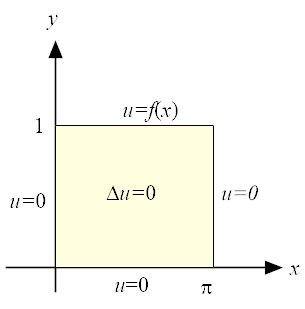



|
 |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
|
|
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
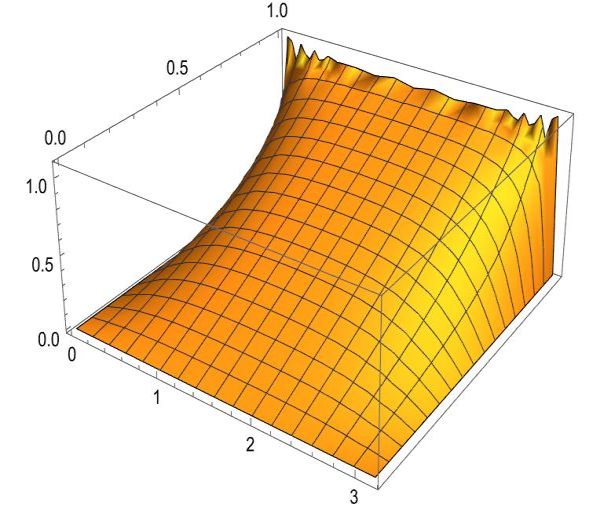 |
| (18) |
| (19) |
| (20) |
|
| (22) |
|
|
|
|
|
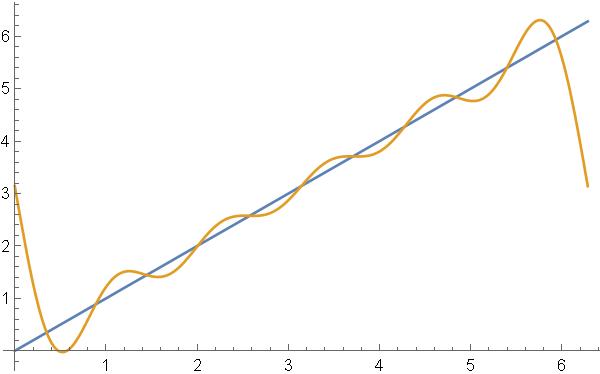
|
|
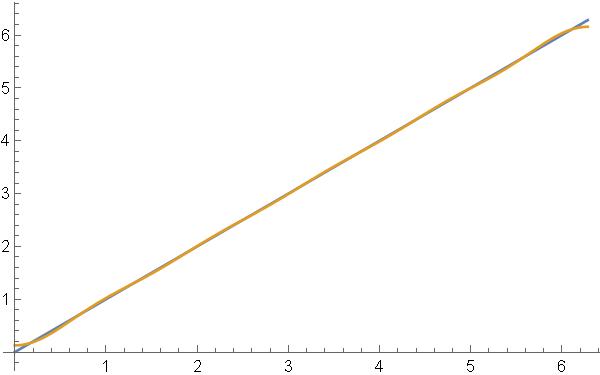
 for (f0, f1, f2, …fN−1)
for (f0, f1, f2, …fN−1)
|
| (28) |
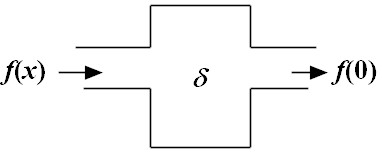 |
| (29) |
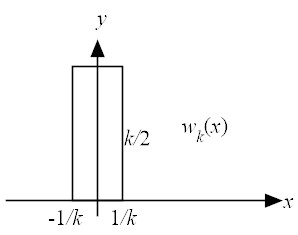 |
|
| (31) |
| (32) |
|
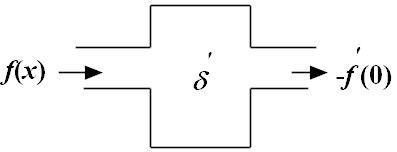 |
| (34) |
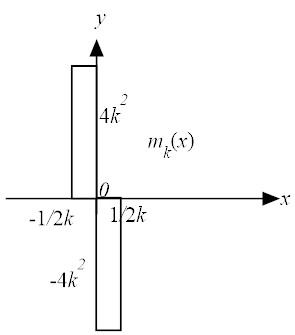 |
|
| (36) |
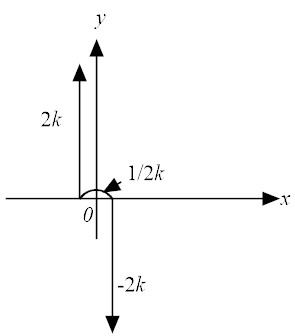 |
| (37) |
|
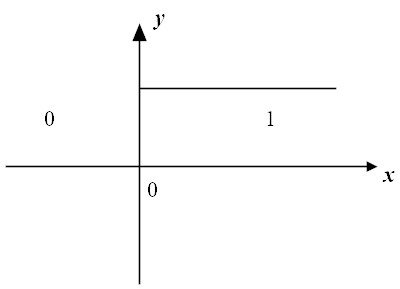
| (39) |
| (40) |
 |
|
| (42) |
|
|
|
|
|
| (46) |
|
|
|
| (47) |
|
| (49) |
| (50) |
|
| (52) |
|
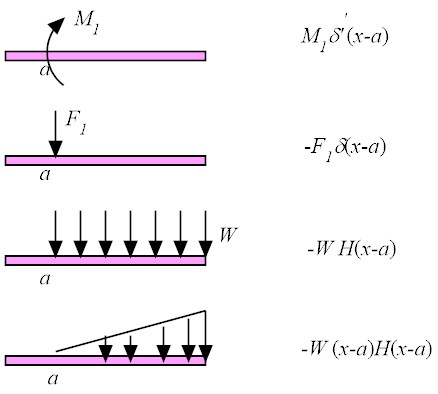
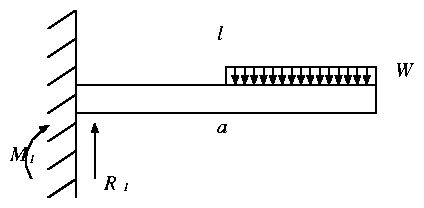
| (58) |
 |
 |
|
|
|



|