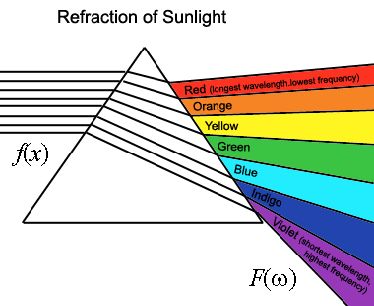



|
|
|
|
| (6) |
| (7) |
| (8) |
| (9) |
 |
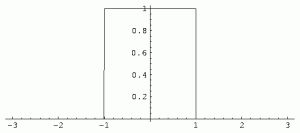 |
|
|
| (12) |
| (13) |
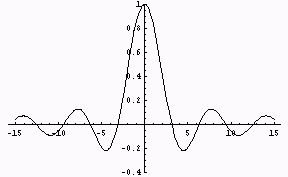 |
|
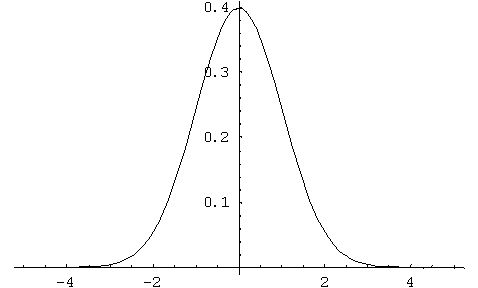 |
|
|
|
|
| (17) |
|
| (20) |
| (21) |
| (22) |
| (23) |
|
| (25) |
|
|
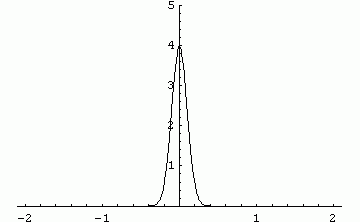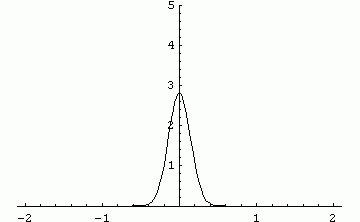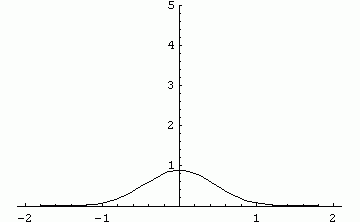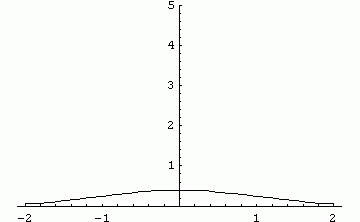 It is seen that a pulse initially at x=0 propagates to x=±∞
instantly at any small t which is the nature (and flaw) of the
diffusion equation.
It is seen that a pulse initially at x=0 propagates to x=±∞
instantly at any small t which is the nature (and flaw) of the
diffusion equation.


