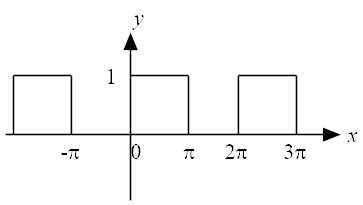



| (1) |
|
|
| (2) |
|
| (4) |
 |
| (5) |
|
|
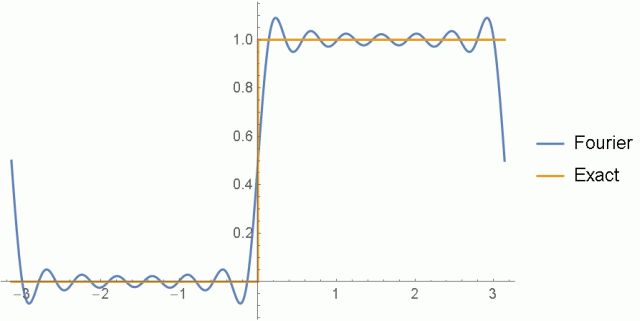 |
| (11) |
| (12) |
| (13) |
| (14) |
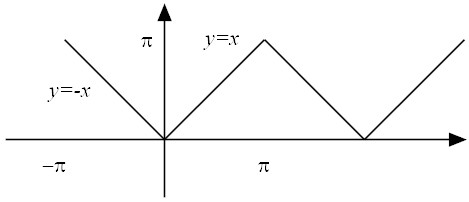 |
| (15) |
|
|
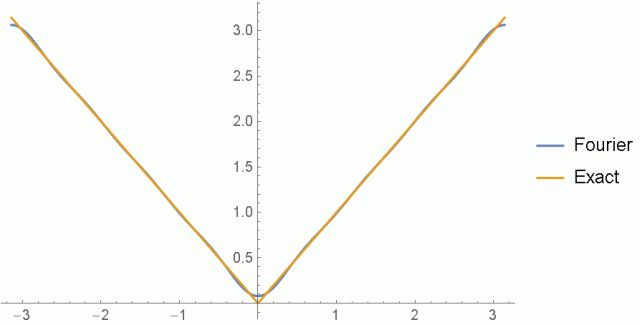 |
| (20) |
| (21) |
|

Examples: Cos[x], Sin[m x], Exp[x], Pi, Infinity, Tan[x] etc.. |
|
|
|
|
|
| (22) |
|
|
| (24) |
 |
| (25) |
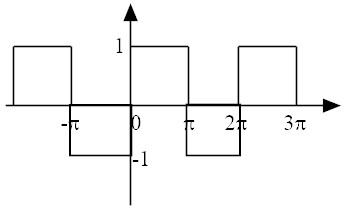 |
| (26) |
| (27) |
|
| (29) |
|
| (31) |
| (32) |
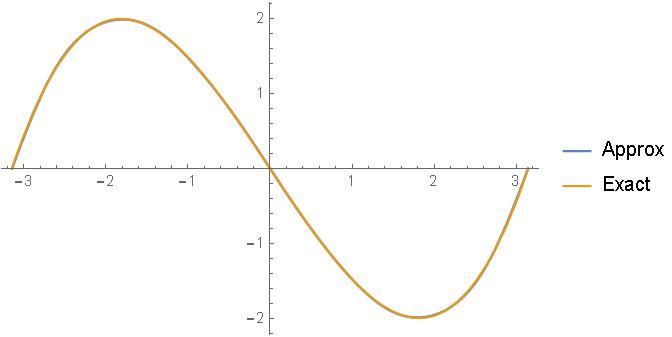 |
| (33) |
| (34) |
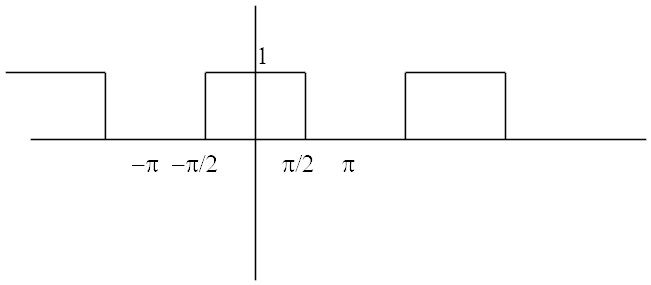 |
| (35) |
| (36) |
|
| (38) |
| (39) |
|
| (42) |
| (43) |
| (44) |
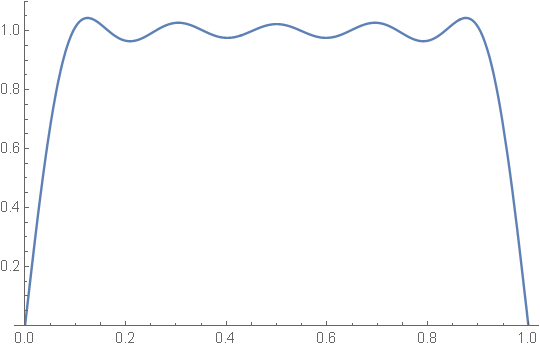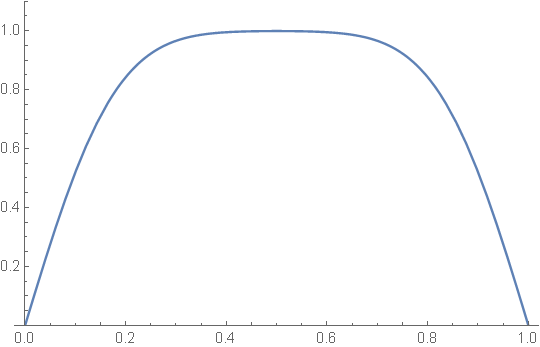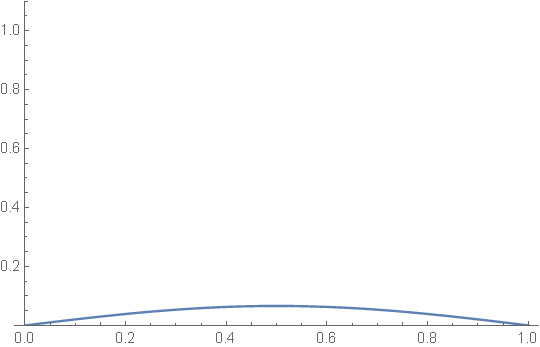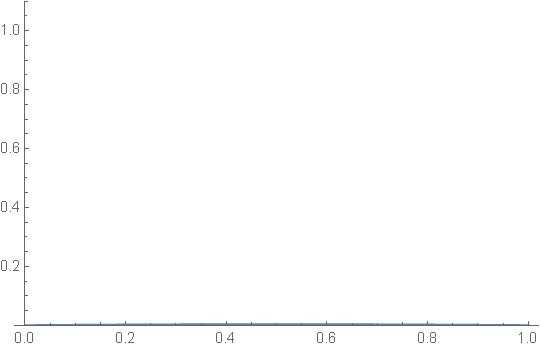
| (45) |
| (46) |
|
|
|



|
|