#10 (09/22/2025)

Divergence theorem (Gauss theorem)

Remember the definition of the divergence operator for 2-D as

div u ≡
lim
∆s→ 0 
⌠
(⎜)
⌡


∂S 
 n ·u dl
∆s
 ,
(1)
where n is the normal to the boundary, ∆s is the surface area of the object, and ∂S is the boundary of the object domain. This definition has an advantage over other definitions as it is independent of the coordinate system.
Equation (1) is approximately written as

⌠
(⎜)
⌡


∂S 
 n·u dl ∼ ∇·u ∆s.
(2)
If Eq.(2) is applied to the two regions below,
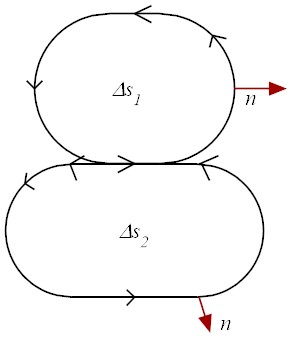gausstheorem.jpg
it follows

⌠
(⎜)
⌡


∂s1 
 n·u dl
 ∼ 
∇·u ∆s1,
(3)
⌠
(⎜)
⌡


∂s2 
 n·u dl
 ∼ 
∇·u ∆s2,
(4)
which can be added together to yield

⌠
(⎜)
⌡


∂(s1 + s2) 
 n·u dl ∼ ⌠
⌡ 		⌠
⌡ 		∇·u dS.
(5)
By repeating this for many small cells and taking limit of ∆si → 0, Eq.(5) becomes

⌠
(⎜)
⌡


∂S 
 n ·u dl = ⌠
⌡ 		⌠
⌡

S 
 ∇·u dS.
(6)
This is called the Gauss divergence theorem.

Verification

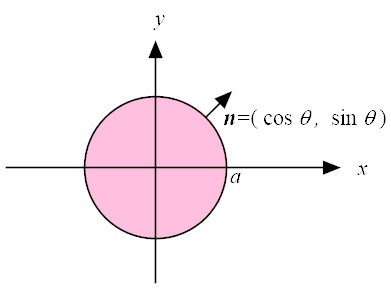
gauss_ex.jpg

u = ⎛
⎜
⎜
⎝
x2 y
x + y
⎞
⎟
⎟
⎠ 		.
(LHS) On the boundary, one can set
x
=
a cos θ
(7)
y
=
a sin θ
(8)
and
On the boundary, one can set
nx
=
cos θ,
(9)
ny
=
sin θ,
(10)
so

n·u = a3 cos3  θsin θ+a sinθ(cos θ+sin θ),
(11)
and

⌠
(⎜)
⌡


∂S 
 n·u dl
=
⌠
⌡ 		2π

0 
 ( a3 cos3  θsin θ+a sinθ(cos θ+ sin θ) )a dθ
=
a2 π1
(12)
(RHS) Use the polar coordinate system, i.e.
x = r cosθ,     y = r sin θ,     dS = r dr dθ.
As

∇·u
=
2 x y + 1,
=
2 r2 cosθsin θ+ 1,
(13)
so

⌠
⌡ 		⌠
⌡

S 
 ∇·u dS
=
⌠
⌡ 		⌠
⌡

S 
 (2 x y + 1) dx dy
=
⌠
⌡ 		2π

0 
 ⌠
⌡ 		a

0 
 (2 r2 cos θsin θ+1) r dr dθ
=
a2 π.
(14)

Alternative interpretation of Gauss theorem

gauss_1d.jpg
The fundamental theorem of calculus postulates that integrations and differentiations are reciprocal to each other, i.e.

⌠
⌡ 		b

a 
 f ′(x) dx = [ f ]ab.
(15)
The right hand side of Eq.(15) can be written as
[ f ]ab
=
−f |x=a + f |x=b
=
(−1) ×f |x=a + (+1) ×f |x=b
=
na  f |x = a + nb  f |x = b
=
(n f) |x=a + (n f) |x=b
=

∑
boundary 
 n f.
(16)
So Eq.(15) can be written as

⌠
⌡ 		b

a 
 f ′(x) dx =
∑
boundary 
 n f.
(17)
Equation (17) can be extended to 2-D as

⌠
⌡ 		⌠
⌡

S 
 ∇f  dS = ⌠
(⎜)
⌡


∂S 
 n f dl.
(18)
Note that both ∇ and n are vectors. If we set f = u (vector), Eq.(18) can be written as

⌠
⌡ 		⌠
⌡

S 
 ∇·u dS = ⌠
(⎜)
⌡


∂S 
 n ·u dl,
(19)
which is the Gauss divergence theorem.
Note that most of the usage of the divergence theorem is to convert a boundary integral that contains the normal to the boundary into a volume (area) integral by replacing the normal (n) by a nabla (∇) to be placed in front of the expression.

⇒

⌠
(⎜)
⌡


∂S 
 …n …dl = ⌠
⌡ 		⌠
⌡

S 
 ∇…dS.
(20)

Integration by parts

Integrating the both sides of

( u v )′ = u ′ v + u v′,
(21)
yields

⌠
⌡ 		b

a 
 ( u v ) ′d x = ⌠
⌡ 		b

a 
  u ′v dx + ⌠
⌡ 		b

a 
  u v ′dx,
(22)
or

[ u v ]ab = ⌠
⌡ 		b

a 
  u ′v dx + ⌠
⌡ 		b

a 
  u v ′dx,
(23)
or
⌠
⌡ 		b

a 
 u′v dx = [ uv]ab −⌠
⌡ 		b

a 
 uv′dx.
(24)
Equation (24) is the 1-D formula for integration by parts.
Equation (24) can be extended to 2D as
⌠
⌡ 		⌠
⌡

S 
 ∇u v dS = ⌠
(⎜)
⌡


∂S 
 u v n dl−⌠
⌡ 		⌠
⌡

S 
 u ∇v dS.
(25)
Example (Green's identity)

⌠
⌡ 		⌠
⌡

S 
 (∇u ·∇v + u ∆v) dS = ⌠
(⎜)
⌡


∂S 
 u ∂v
∂n
 dl.
(26)
Proof:
Rewrite the right hand side of Eq.(26) as
⌠
(⎜)
⌡


∂S 
 u ∇v ·n d l,
(27)
which is a boundary integral with n. Therefore, according to the Gauss theorem, it follows

⌠
(⎜)
⌡


∂S 
 u ∇v ·n d l
=
⌠
⌡ 		⌠
⌡

S 
 ∇·(u ∇v ) d S
=
⌠
⌡ 		⌠
⌡

S 
 ( ∇u ·∇v + u ∇·∇v) d S
=
⌠
⌡ 		⌠
⌡

S 
 ( ∇u ·∇v + u ∆v) d S .
(28)
Examples
  1. Heat conduction
    The balance of energy is stated as

    ⌠
    ⌡     		⌠
    ⌡

    S 
    		 ρCp ∂T
    ∂t
    		 dS = ⌠
    (⎜)
    ⌡


    ∂S 
    		 (−n) ·h dl,
    		(29)
    where ρ is the mass density, Cp is the specific heat, h is the heat flux across the boundary of the control surface.
    Using the Gauss theorem, the right hand side of Eq.(29) becomes

    ⌠
    (⎜)
    ⌡


    ∂S 
    		 (−n) ·h dl = −⌠
    ⌡     		⌠
    ⌡

    S 
    		 ∇·h dS,
    		(30)
    so it follows
    ⌠
    ⌡     		⌠
    ⌡

    S 
    		 ρCp ∂T
    ∂t
    		 dS = −⌠
    ⌡     		⌠
    ⌡

    S 
    		 ∇·h dS,
    		(31)
    or
    ρCp ∂T
    ∂t
    		 + ∇·h = 0.
    		(32)
    Using Fourier's law,
    h = − k ∇T,
    		(33)
    where k is the thermal conductivity, Eq.(32) becomes
    ρCp ∂T
    ∂t
    		 = ∇·(k ∇T).
    		(34)
  2. Equilibrium equation in static elasticity
    The balance of force for continua is stated as

    ⌠
    (⎜)
    ⌡


    ∂S 
    		 t dl+ ⌠
    ⌡     		⌠
    ⌡

    S 
    		 b dS=0,
    		(35)
    where t is the surface traction force and b is the body force. The surface traction force t is the contribution of the stress tensor, σ, in the direction of n as
    t = σ·n,
    		(36)
    so Eq.(35) becomes
    ⌠
    (⎜)
    ⌡


    ∂S 
    		 σ·n dl+ ⌠
    ⌡     		⌠
    ⌡

    S 
    		 b dS=0,
    		(37)
    or
    ⌠
    ⌡     		⌠
    ⌡

    S 
    		 ∇·σdS + ⌠
    ⌡     		⌠
    ⌡

    S 
    		 b dS=0,
    		(38)
    or

    ∇·σ+ b = 0,
    		(39)
    which is known as the equation of equilibrium. For small elastic deformation,
    σ = C ∇u,
    		(40)
    where C is the elastic modulus and u is the displacement, Eq.(39) becomes
    ∇·( C ∇u) + b=0,
    		(41)
    which is known as the Navier's equation 2.
  3. Green's second identity
    ⌠
    ⌡     		⌠
    ⌡

    S 
    		 (u ∆v − v ∆u) dS = ⌠
    (⎜)
    ⌡


    ∂S 
    		 ⎛
    ⎝     		u ∂v
    ∂n
    		 − v ∂u
    ∂n
    		⎞
    ⎠     		dl.
    From the first Green's identity,
    ⌠
    ⌡

    S 
    		 (∇u ·∇v + u ∆v) dS
    =
    ⌠
    (⎜)
    ⌡


    ∂S 
    		 u ∂v
    ∂n
    		 dl,
    		(42)
    ⌠
    ⌡

    S 
    		 (∇v ·∇u + v ∆u) dS
    =
    ⌠
    (⎜)
    ⌡


    ∂S 
    		 v ∂u
    ∂n
    		 dl.
    		(43)
    Subtracting Eq.(43) from Eq.(42) gives the second Green's identity. This identity is used to derive solutions to Poisson's equation (∆u = −ρ).

Footnotes:

1
Integrate with respect to
from to .

Enter a^4 Cos[x]^3 Sin[x] +a^2 Sin[x]Cos[x]+a^2 Sin[x]^2, x, 0, 2 Pi (you can copy and paste with the mouse.)

2 Each quantity is a tensor.

File translated from TEX by TTH, version 4.03.
On 21 Sep 2025, 13:52.