Sqrt[1 + 4 u^2] u 0 1exactly (case sensitive, square bracket) in the boxes then press the query button.

|
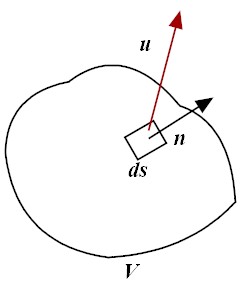
Surface area element
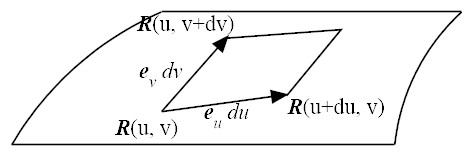 |
|
|
|
|
|
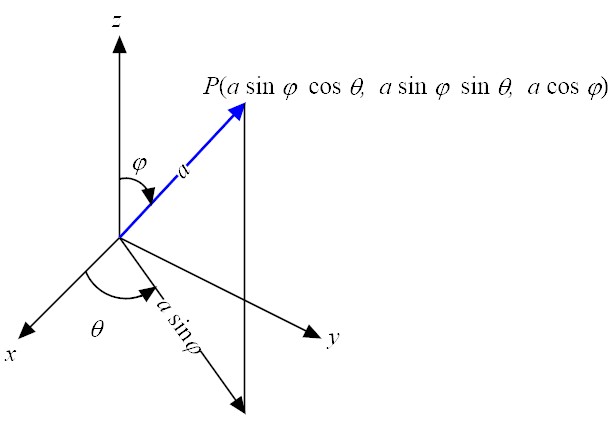
Example of surface integral
As an example of surface integrals, we attempt to compute the surface area of a sphere x2 + y2 + z2 = a2. By setting x = u and y = v, a position vector on the sphere is expressed as
| (9) |
|
| (12) |
| (13) |
| (14) |
 |
| (15) |
| (16) |
|
|
|
z = f(x, y)
If the equation of a curved surface is given as
| (25) |
| (26) |
| (27) |
| (28) |
Volume
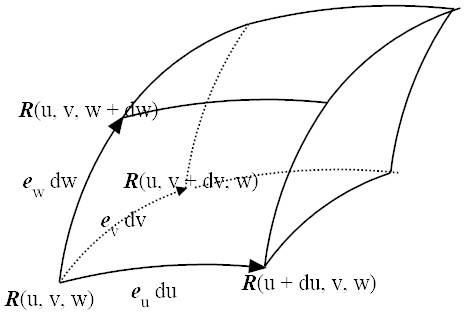 The volume element of the parallelepiped spanned by the three vectors above
can be expressed as3
The volume element of the parallelepiped spanned by the three vectors above
can be expressed as3
| (29) |
 |
| (30) |
| (31) |
| (32) |
| (33) |
|
Summary
- Length of Arc
dl =
√
eu ·eudu = |eu | du. - Area
d s = ⎛
⎥
√| eu ·eu, eu ·ev eu ·ev, ev ·ev | du dv = |eu ×ev| du dv. - Volume
d v = ⎛
⎥
⎥
√⎢
⎢
⎢
⎢
⎢eu ·eu, eu ·ev, eu ·ew ev ·eu, ev ·ev, ev ·ew ew ·eu, ew ·ev, ew ·ew ⎢
⎢
⎢
⎢
⎢du dv dw = |eu ·(ev ×ew) | du dv dw.
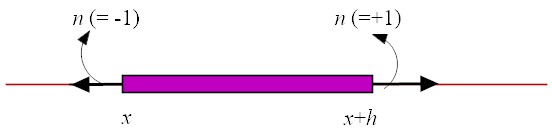
Divergence
The divergence operator can be defined on a vector, u, by
| (35) |
1-D
 |
|
2-D
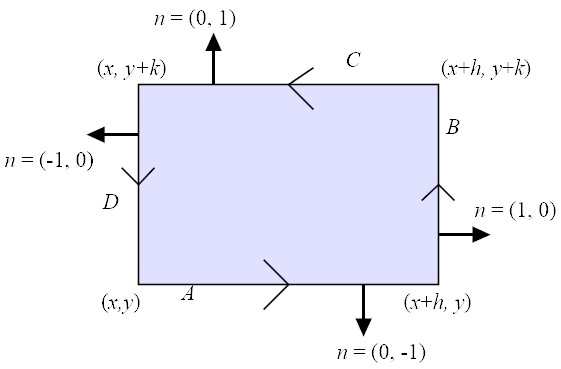 |
Path A
Along the path A, n = (0,−1) so n·u = − uy(x, y). Thus
| (39) |
Path B
Along the path B, n = (1, 0) so n·u = ux(x + h, y). Thus
| (40) |
Path C
Along the path C, n=(0,1) so n·u = uy(x,y+k). Thus
| (41) |
Path D
Along the path D, n = (−1, 0) so n·u = −ux(x, y). Thus
| (42) |
| (43) |
|
3-D
From the result in 2-D, it is obvious that the divergence operator in 3-D is expressed as
| (46) |
| (47) |
| (48) |
Gradient
Similar to the divergence operator, the gradient operator is defined as
| (49) |
By applying this definition to a rectangular element in the Cartesian coordinate system, one can obtain
| (50) |
| (51) |
| (52) |
Curl
The curl operator is defined on a 3-D vector as
| (53) |
|
|



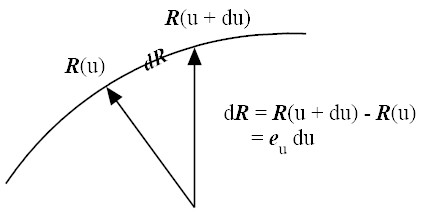 The length of a curved line from u = u to u = u + du can be
computed by carrying out integration of ds (line segment)
The length of a curved line from u = u to u = u + du can be
computed by carrying out integration of ds (line segment)
 Solution
As
Solution
As