#07 (09/10/2025)

Implicit functions

If the relationship between x and y is given implicitly as

f(x, y) = 0,
(1)
it is still possible to express y as a function of x by Taylor series about x = a as

y(x) = y(a) + y′(a)(x − a) + y"(a)
2!
 (x − a)2 + y"′(a)
3!
 (x − a)3 + …
(2)
if y(a), y′(a), y"(a) … are known. One can differentiate f(x, y) = 0 with respect to x to get y′(x) without explicitly solving f(x, y) = 0 for y(x) as

fx (x, y) + fy(x, y) y′(x) = 0,
(3)
or

y′(x) = − fx(x,y)
fy(x,y)
 .
(4)
Once y′(x) is obtained, y"(x) can be derived by differentiating the both sides of y′(x) with respect to x again 1 as

y"(x)
=
− (fxx + fxy y′)fy − fx (fyx + fyyy′)
fy2
=
−
⎛
⎝ 		fxx + fxy ( − fx
fy
 )⎞
⎠ 		fy − fx ⎛
⎝ 		fyx + fyy( − fx
fy
 )⎞
⎠
fy2
=
2fx fy fxy −fx2 fyy − fy2 fxx
fy3
 ,
(5)
and other higher order derivatives can be obtained in a similar manner.
It is seen that for y = y(x) to exist at x = x0, the denominator of fy must not vanish, i.e.
∂f
∂y
 (x0, y0) ≠ 0.
(6)

Example

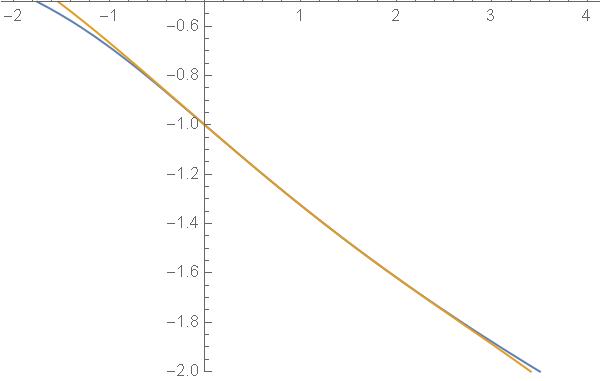
Expand y(x) about x = 1 up to and including second order for
f(x, y) ≡ x y −y3 − 1 = 0.
(7)
Solution: The Taylor series of y(x) about x=1 is
y(x) = y(1) + y′(1)(x − 1) + y"(1)/2! (x − 1)2 + …
(8)
By substituting x = 1 into x y − y3 − 1 = 0, one gets y(1) = −1.32 … by solving y − y3 − 1 = 0 (there are two other complex roots but are not considered here). Next, by differentiation x y − y3 − 1 = 0 with respect to x (note that y is a function of x), one gets y + x y′− 3 y2 y′ = 0 which can be solved for y′ as y′ = y/(3 y2 − x). This can be further differentiated with respect to x as y" = (y′(3y2 − x) − y(6 y y′−1))/(3 y2 − x)2 so it is possible to obtain y(1), y′(1), y"(1), ... sequentially. Finally, one obtains

y(x) = −1.32472 −0.310629 (x−1) +0.0170796 (x−1)2+0.00114503 (x−1)3 −0.00128188 (x−1)4+ …
(9)
implicit_diff.jpg

Application:Lagrange multiplier

As an application of the theory of implicit functions, the Lagrange multiplier method is discussed here. We want to extremize f(x, y) subject to the constraint, g(x, y) = 0. Assuming g(x, y) = 0 can be solved for y as y = y(x), this is substituted into the object function of f(x, y) as f(x, y(x)) thus we can look at f(x, y(x)) as a function of x. The candidates of x's to extremize f can be obtained by differentiating f with respect to x as
f′(x) = fx + fy y′ = 0,
(10)
where y′ in Eq.(10) can be obtained from g(x, y) = 0 as
y′ = − gx
gy
 .
(11)
Substituting Eq.(11) to Eq.(10) yields

fx
gx
 = fy
gy
 ≡ λ,
(12)
where λ is a newly introduced parameter called the Lagrange multiplier. The development above implies that when extremizing f(x, y) subject to g(x, y) = 0, instead of working on f(x, y), one can try extremizing

f* ≡ f(x, y) − λg(x, y),
(13)
without any constraint, i.e. partially differentiating Eq.(13) with respect to x, y and λ as
∂f*
∂x
=
fx − λgx = 0,
(14)
∂f*
∂y
=
fy − λgy = 0,
(15)
∂f*
∂λ
=
−g = 0.
(16)
The above equations form a set of simultaneous equations for x, y and λ.

Example 1

Find the shortest distance from the origin (0, 0, 0) to the plane, a x + b y + c z = d.

f(x, y, z) = x2 + y2 + z2 → min
(17)

subject to g(x, y, z) = a x + b y + c z − d = 0.
(18)
Instead of minimizing f(x, y, z) with the constraint, one can try minimizing f*(x, y, z) ≡ f(x, y, z) − λg(x, y, z) with respect to x, y, z and λ without any constraint.

∂f*
∂x
=
2 x− λa = 0,
(19)
∂f*
∂y
=
2 y− λb = 0,
(20)
∂f*
∂z
=
2 z− λc = 0,
(21)
∂f*
∂λ
=
a x + b y + c z − d = 0.
(22)
Solving the above set of simultaneous equations yields

x
=
λa
2
(23)
y
=
λb
2
(24)
z
=
λc
2
(25)
λ
=
2 d
a2 + b2 + c2
 ,
(26)
or equivalently

x
=
ad
a2 + b2 + c2
(27)
y
=
bd
a2 + b2 + c2
(28)
z
=
cd
a2 + b2 + c2
 ,
(29)
so the minimum distance is

√
 
x2 + y2 + z2
 
 = d

√
a2 + b2 + c2
 .
(30)
Alternative approach: Read the problem as Find the shortest distance from the origin (0, 0, 0) to the plane, a x + b y + c z = d.
lagrange_multi.jpg
The plane, a x + b y + c z = d, is also expressed as

a·x = d,
(31)
where a = (a, b, c) and x = (x, y, z). Equation (31) implies that the vector a is perpendicular to the plane (as was shown in class). Hence, the vector from the origin that minimizes the distance to the plane must be expressed as

x = t a,
(32)
where t is a parameter. By substituting Eq.(32) into Eq.(31), one obtains

a ·ta = t a·a = d.
(33)
Hence, t can be solved as
t = d
a·a
 .
(34)
From Eq.(32), it follows
x = d
a·a
 a,
(35)
and the length of x is

| x |
=
| d
a·a
 a |
=
d
|a|2
 |a|
=
d
|a|
=
d

√
 
a2 + b2 + c2
 
.
(36)

Example 2

Find the shortest distance from (1, 0) to x3 − 2 y2 = 0.
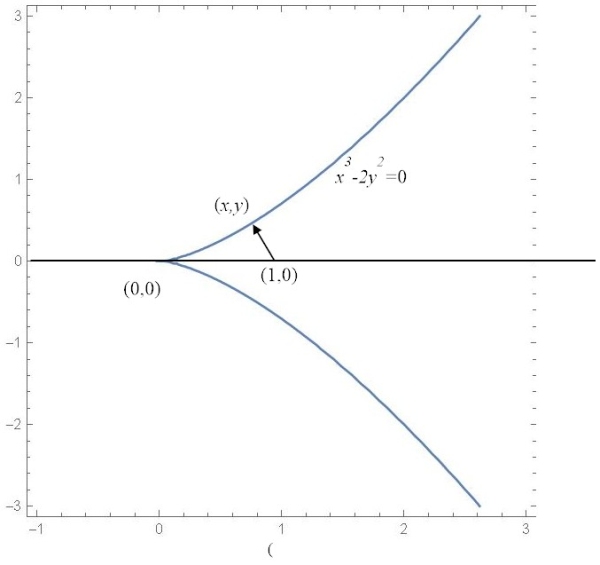lagrange_1.jpg
(Solution) Let
f* ≡ (x −1)2 + y2 − λ(x3 − 2 y2),
it follows

∂f*
∂x
=
2 (x − 1) − 3 x2 λ = 0,
(37)
∂f*
∂y
=
2 y + 4 y λ = 0,
(38)
∂f*
∂λ
=
− x3 + 2 y2 = 0.
(39)
The above equations can be solved as (real roots)

(x, y, λ) = ( 2
3
 , 2
3 √3
 , − 1
2
 )    or     ( 2
3
 , − 2
3 √3
 , − 1
2
 ),
(40)
both of which yield

d =
√
 
(x−1)2 + y2
 
 =   ⎛
√
7
27
 
  ∼ 0.509175.
(41)
Sample MATLAB/Octave code: 
x=1; y=1; lambda=1;

for i=0:10
 eqs=[ 2*(x-1)-3*x*x*lambda ; 2*y+4 *y *lambda ; -x^3+2*y*y];

 jacob=[2-6*x*lambda, 0, -3*x*x; 0, 2+4*lambda, 4*y; -3*x*x, 4*y, 0];

 right=inv(jacob)*eqs;

 x=x-right(1);
 y=y-right(2);
 lambda=lambda-right(3);
end;

fprintf('%f %f %f\n', x, y,lambda);
fprintf('%f', sqrt((x-1)^2+y^2));
Online C compiler
Online MATLAB/Octave
Wolfram Alpha

Vector Analysis

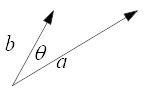
Scalar product (inner product, dot product)

The scalar product between the two vectors, a and b, is defined as

a·b = a b cos θ,
(42)
where θ is the angle between the two vectors.
innerpro.jpg
The following properties can be derived based on the definition of Eq.(42).
  1. a ·b = b ·a
  2. c a ·b = a ·c b = c (a ·b)
  3. a ·(b + c ) = a ·b + a ·c
It is possible to derive the scalar product in terms of the components of a vector by introducing the base vectors, ex and ey. Note that

ex·ex
=
ey·ey
=
1,
ex·ey
=
ey·ex
=
0.
(43)
Using Eq.(43), the scalar product of two vectors in components is
a·b
=
(ax ex +ay ey )·(bx ex +by ey )
=
ax bx ex ·ex + ax by ex ·ey + ay bx ey ·ex + ay by ey ·ey
=
ax bx + ay by.
(44)
The definition of Eq.(42) is a preferred form as it is independent of the coordinate system.

Vector product (cross product)

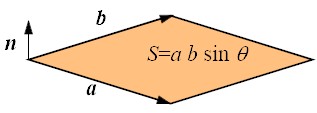
The vector product is defined between two vectors in 3-D as

a×b ≡ S n,
(45)
where S is the area of the parallelogram spanned by the two vectors and n is the unit vector whose direction is in the right hand system as shown in the figure.
crosspro.jpg
The following properties can be derived based on the definition of Eq.(45).
  1. a ×b = −b ×a
  2. c a ×b = a ×c b = c (a ×b)
  3. a ×(b + c ) = a ×b + a ×c
Note that a×a = 0 (no area by two identical vectors).
The relationship among 3-D base vectors is summarized as

ex×ey
=
−ey×ex
=
ez
ey×ez
=
−ez×ey
=
ex
ez×ex
=
−ex×ez
=
ey,
(46)
and

ex ×ex = ey ×ey = ez ×ez = 0.
(47)
Using the relationship above, the vector product is expressed in components as
a×b
=
(ax ex +ay ey +az ez )×(bx ex +by ey +bz ez )
=
ax bx ex×ex+ax by ex×ey+ax bz ex×ez+ …
=
…
=
⎢
⎢
⎢
⎢
⎢
ex
ey
ez
ax
ay
az
bx
by
bz
⎢
⎢
⎢
⎢
⎢ 		.
(48)

Equation of plane (application of dot product)

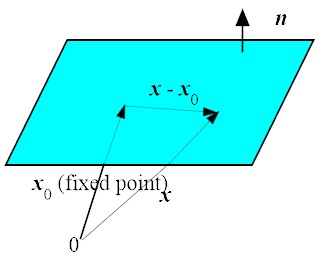eqplane.jpg
The relationship among x0 (fixed point), x (moving point) and n (normal, fixed vector) is

n ·(x−x0) = 0.
(49)
So the equation of a plane is expressed as
n ·x
=
n ·x0
=
c.
(50)
Note that c represents the shortest distance between the plane and the origin.

Triple products

There are two types of vector products, scalar triple product and vector triple product, whose main usage is found in vector analysis.

Scalar triple products, a·(b×c)

a·(b×c) = a·S n = S a cosθ = S h represents the volume of the parallelepiped spanned by the three vectors, a, b and c. Note the cyclic relationship below.
a·(b×c) = b·(c×a) = c·(a×b)
triplepro.jpg

Vector triple products, a ×(b×c)


a ×(b×c) = (a·c)b − (a·b)c.
Note that the right hand side is a combination of b and c both of which are inside the parentheses in the left hand side. The one that is in the middle (b) comes first.
Exercise
  1. a×( b×c) +b×( c×a) +c×( a×b) = ?
  2. (a×b)·(c×d) = ?

Footnotes:

1
⎛
⎝ 		u
v
⎞
⎠ 		′

 
 = u′v − u v′
v2
 .


File translated from TEX by TTH, version 4.03.
On 09 Sep 2025, 23:05.