UTA ME5331 Lecture 01
#01 (08/18/2025)

Limit and Continuity

In the ϵ-δ language,

lim
x→ x0 
 f(x) = a,
(1)
is equivalent to the following statement:
To each ϵ > 0, there exists a δ > 0 such that |f(x) − a| < ϵ whenever 0 < |x − x0| < δ.
The advantage of this definition is that it does not require any intuition of how big or how small ϵ or δ should be.
Example:
f(x) = ⎧
⎪
⎨
⎪
⎩
x2
    x ≠ 2
8
    x = 2
We claim that limx→ 2f(x) = 4, not 8 as for an arbitrarily given ϵ > 0, one can always choose δ = √{4 + ϵ} − 2 even though f(2) = 8.
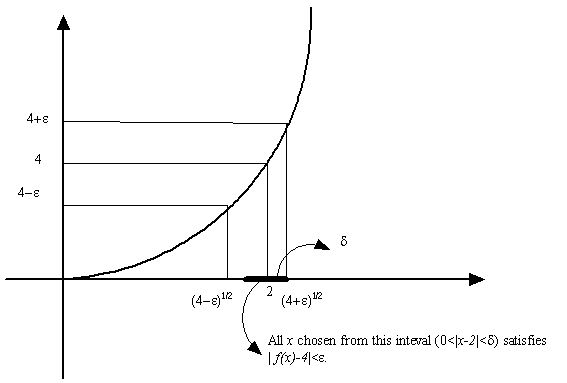eps-delta.jpg
In engineer's language, it suffices to say that limx→x0f(x) = a means that f(x) can be arbitrarily close to a when x is sufficiently close to x0 (Note: x does not have to be equal to x0).
If limx→ x0 f(x) exists and is equal to f(x0), we say that f(x) is continuous at x = x0. Obviously, if f(x) is continuous at x0, it has a limit as x→ x0 but the converse is not true.
Example Show that

lim
x→ 0 
 f(x) = 0,
if
f(x) ≡ 1
x
 − 1
sin x
 .
Theorem (L'Hospital): If f(a) = g(a) = 0, f(x) and g(x) are differentiable at x=a, and g′(x) ≠ 0, then,

lim
x→ a 
 f(x)
g(x)
 =
lim
x→ a 
 f′(x)
g′(x)
(2)
(Proof):

lim
x→ a 
 f(x)
g(x)
=

lim
x→ a 
 f(x) − f(a)
g(x) − g(a)
=

lim
x→ a 
f(x) − f(a)
x − a
g(x) − g(a)
x − a
=
f′(a)
g′(a)
 .
(3)
Note that the above theorem is also applicable when you have [(∞)/(∞)] (choose f*(x) = 1/f(x)).
Some exercise

(a)
lim
x→ 0 
 1 − cos x
x2
(b)

lim
x→ ∞ 
 ex
xn
(c)
lim
x→ +0 
 xx
(d)

lim
x→ 0 
 cos x
x + 1
Another example of somewhat exotic function (Dirichlet function):
f(x) =
lim
m→ ∞,n→ ∞ 
 cos 2n(m! πx).
(4)
As shown in class, this function is 1 when x is a rational number and 0 when x is an irrational number. It is difficult to sketch this function. Any usage of such a function ? This is an example of functions that is integrable in the sense of Lebesgue but not in the sense of Riemann.


File translated from TEX by TTH, version 4.03.
On 18 Aug 2025, 13:36.