Octave (Poor man's MATLAB)

MATLAB is a powerful application package for scientific/engineering tasks that combines the easiness of hand-held calculators and the versatility of C programming. MATLAB can do (.... blurbs here.....) and is widely used in many engineering schools including UTA. The drawback of MATLAB is its price.
GNU Octave is a high-level language that is mostly compatible with MATLAB. It may also be used as a batch-oriented language.

Download page (Windows and Mac)

Direct Link to the Windows executable (ver 6.4, 600 MB)

Basics

  1. No distinction between integers and floating points.
  2. Variable names are case-sensitive.
  3. The index of an array begins at 1 (0 for C).
  4. Everything is processed as a matrix including a single variable. An interval is also entered by a matrix.
  5. The square brackets denote vectors/matrices (i.e. [3 4 1], [1 2 3; 4 5 6; 7 8 9]).
  6. Everything after % and # is a comment.
  7. Statements ending with ; (semicolon) do not echo back.

Basic operations

clc % clears screen
1+3
2^12
(3+2*i)*(2-4*i) % complex algebra
abs(4-3*i) %absolute value
sin(pi)
cos(2*pi)
log(2.718) %natural logarithm
log2(1024)
log10(1000)
format long
sqrt(5)
pi
format short
sqrt(3)

Variables

a=20.0
b=a-sin(3);
a+b
clear a
a
  1. Variable names are case sensitive.
  2. You should avoid using reserved names (such as sum) for variables.

Reserved constants

i %imaginary number
j % same as i
clock % current time (six elements)
date % current date
pi %3.14156
eps %smallest tolerance number in the system

format long
pi
pi=2.14
pi
clear pi
pi
If you use above symbols as your own variables, they no longer represent the original pre-assigned values. This also applies to built-in functions such as sin, sum, cos, etc ...

Vectors/matrices

v1=[1 2 3] % defines a 3-D row vector.
v1=[1, 2, 3] % Same as above. Separator is either space or comma


v2=[1;2;3] % this defines a column vector.
v2=v1' %transpose of v1, i.e. column vector

m1=[1 2 3;4 5 6;7 8 9] %defines a 3x3 matrix
m1=[1,2,3;4,5,6;7,8,9]; %semicolon suppresses echo

m2=[-4 5 6; 1 2 -87; 12 -43 12];

m2(:, 1) % Extracts the first column
m2(2, :) % Extracts the second row

m2(2,3)=10; % Assigns 10 to the (2,3) element of m2.

m1*v2 %matrix multiplication

inv(m1) %inverse of m1

[vec, lambda] = eig(m1) % eigenvectors and eigenvalues of m1

m1\m2 % inverse of m1 times m2, same as inv(m1)*m2

m1*v2 % matrix m1 times vector v2

a=eye(3) % 3x3 identity matrix

a=zeros(3) % 3x3 matrix with 0 as components

a=ones(3) % 3x3 matrix with 1 as components

det(m1) % determinant of m1
  1. You can use the space and the comma interchangeably.
  2. Solving three simultaneous equations
    ⎛
    ⎜
    ⎜
    ⎜
    ⎝
    1
    4
    5
    8
    1
    2
    6
    9
    −8
    		⎞
    ⎟
    ⎟
    ⎟
    ⎠     		⎛
    ⎜
    ⎜
    ⎜
    ⎝
    x
    y
    z
    		⎞
    ⎟
    ⎟
    ⎟
    ⎠     		= ⎛
    ⎜
    ⎜
    ⎜
    ⎝
    4
    7
    0
    		⎞
    ⎟
    ⎟
    ⎟
    ⎠
    can be done by 
     a=[1 4 5; 8 1 2; 6 9 -8];
 b=[4; 7; 0];
 sol2 = inv(a)*b
   % or 
 sol2 = a\b
Although Octave/MATLAB can perform mathematical operations other than linear algebra (matrices/vectors), its underlying design principle is to process numbers as matrices (including vectors). This includes defining an interval range as a row vector and the corresponding function values. 
x=[1: 2 :10]; % a sequence between 1 and 10 with an increment of 2.
x=linspace(1, 9, 5); a sequence between 1 and 9 with equidistant 5 entries

y=x;

z=x * y % error
z = x .* y; %works

z = x / y ; %error
z = x ./y ; % works

Graph

x=[0:0.1:10]; %initial value, increment, final value
y=sin(x);
plot(x, sin(x)); %calls Gnuplot


x=linspace(0,2, 20) % between 0 and 2 with 20 divisions
plot(x, sin(x))
%%%%%%%%%%%%%%%%%%
x=[0: 0.2 : 10];
y=1/2 * sin(2*x) ./ x;
xlabel('X-axis');
ylabel('sin(2x)/x');
plot(x, y);

close;
%%%%%%%%%%%%%%%%%
t=[0: 0.02: 2*pi];
plot(cos(3*t), sin(2*t))

%%%%%%%%%%%%%%%%%%%%
x=[0: 0.01: 2*pi];
y1=sin(x);
y2=sin(2*x);
y3=sin(3*x);
plot(x, y1, x, y2,x, y3);
%%%%%%%%%%%%%%
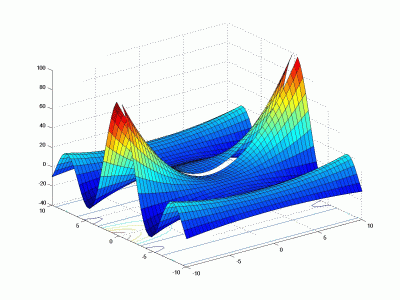
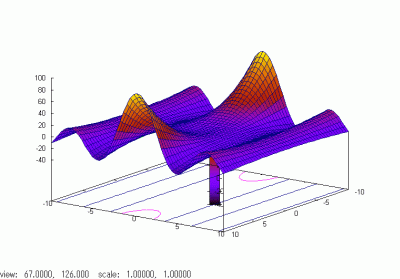
xx=[-10:0.4:10];
yy=xx;
[x,y]=meshgrid(xx,yy);
z=(x .^2+y.^2).*sin(y)./y;
mesh(x,y,z)
surfc(x,y,z)
contour(x,y,z)
close

Octave generated graph.


MATLAB generated graph

Polynomial

a=[1 2 3 4 5] % defines x4+2x3+3x2+4x+5
r=roots(a) % solves x4+2x3+3x2+4x+5=0.

I/O

disp(a) 
disp('Enter a number = ')
a=input('Enter a number =');
fprintf('The solution is %f\n', a);# %f and %d are available but not %lf

File/Directory handling

cd c:\temp
cd 'c:\Documents and Settings\user\My Documents'

pwd % present working directory
cd % back to home directory

myownfile % loading a script m-file named "myownfile.m"
save myown.txt a, b  % saves variables "a" and "b" to a file "myown.txt"
load myown.txt

M-files

  1. Function m-files
    A script file that has the definition of your own function saved under the same name as the function name with m as the extension
    Automatically loaded into Octave/MATLAB as if it were a built-in function. 
    function y=myfunction(x)
y=x^3-x+1;

    function [x, y]=myfunction2(z)
x=z^2;
y=z^3;

    [a,b]=myfunction2(3);
  2. Script m-files
    A batch files that contain a set of statements that you would otherwise type from the keyboard.
    To load a script m-file, type the file name (without extension, m) from the prompt.

Conditional statement

if a>2 
 disp('a is larger than 2')
end

for k=0:2:10
 disp(2*k)
end

Sketch of comparison between C and Octave (MATLAB)

Quadratic equation 
/* This program computes roots 
for quadratic equation. */
#include <stdio.h>
#include <math.h>

int main()
{
double a, b, c, disc, x1, x2;

printf("Enter 3 coeffs separated by space =");
scanf("%lf %lf %lf", &a, &b, &c);

disc=b*b-4*a*c;

if (disc<0) 
  { printf("Imaginary roots !\n"); return 0;}

x1= (-b + sqrt(disc))/(2*a);
x2= (-b - sqrt(disc))/(2*a);

printf("The roots are %lf and %lf. \n", x1, x2);

return 0;
}

a=input('Enter a = ');
b=input('Enter b = ');
c=input('Enter c = ');

disc=b^2-4*a*c;

if disc<0 
 disp('Imaginary roots !'); 
 return;
end;

x1=(-b-sqrt(disc))/(2*a);
x2=(-b+sqrt(disc))/(2*a);

fprintf('Roots are %f %f.\n', x1,x2);
Series summation 
#include <stdio.h>
#include <math.h>

int main()
{
  int i;
  double sum = 0.0;
  for (i=0; i<1000; i++) 
    sum+=pow(-1,i)/(double)(2*i+1);
  printf("approx= %f true value= %lf\n ",
   4*sum, 4*atan(1.0));
return 0;
}


sum=0;

for k=0:1000 
 sum=sum+(-1)^k/(2*k+1); 
end

fprintf('Approx and exact values = %f %f.\n', 4*sum, 4*atan(1));
%% Note that "sum" is a reserved function in MATLAB/Octave.
Array 
#include <stdio.h>
#include <math.h>

#define N 10

int main()
{
  float x[]={ -4.0, 1.2, 1.3, 2.5, -12.7, 
   9.0, 1.41, 65.2, -2.1, 2.36};
  int i;
  float sum = 0.0, average, variance;

  for (i=0; i<N; i++) sum+=x[i];
  average=sum/N;

  for (i=0; i<N; i++) 
   variance += pow(x[i]-average, 2);
  variance = variance/(N-1);

  printf("avg.= %f std. dev. = %f \n ",
    average, sqrt(variance));
  return 0;
}




N=10;
x=[-4 1.2 1.3 2.5 -12.7 9 1.41 65.2 -2.1 2.36];
sum=0;

for k=1:N
 sum=sum+x(k)
end

ave=sum/N;

var=0;
for k=1:N 
 var=var+(x(k)-ave)^2
end

var=var/(N-1);

fprintf('Average = %f, Standard deviation= %f.\n', ave, sqrt(var));
Functions 
#include <stdio.h>
#include <math.h>
#define EPS 1.0e-6

double f(double x)
{
	return x*x-2;
}

double fp(double x)
{
	return 2*x;
}

double newton(double x)
{
	return x - f(x)/fp(x);
}

int main()
{
	double x1, x2;
	int i;

	printf("Enter initial guess  =");
	scanf("%lf", &x1);

	if (fp(x1)==0.0) {
		printf("No convergence.\n");
		return;
	}

	for (i=0;i<100;i++)
	{
		x2=newton(x1);
		if (fabs(x1-x2)< EPS) break;
		x1=x2;
	}

	printf("iteration = %d\n", i);
	printf("x= %lf\n", x1);
	return 0;
}
 
function y=f(x)
y=x*x-2;
%
% Save this file as f.m
%
   
function y=fp(x)
 y=2*x;
%
% Save this file as fp.m
%
   
function y=newton(x)
 y=x-f(x)/fp(x);
%
% Save this file as newton.m
%
    
x1=input('Enter initial guess = ');

if fp(x1) <eps disp('No convergence !');return; end

for i=0:1:99 
 x2=newton(x1);
 if abs(x1-x2)<1e-10 break; end
 x1=x2;
end

fprintf('Iteration = %d\n', i);
fprintf('x = %f\n', x1);
File handling 
#include <stdio.h>
int main()
{
   FILE *fp1, *fp2; 
   float a,b,c;
   fp1=fopen("junk1.dat","r");
   fscanf(fp1, "%f", &a);
   fclose(fp1)

   fp2=fopen("junk2.dat","w");
   fprintf(fp2,"This is the first file.\n");
   fclose(fp2);

   return 0;
}


fp1=fopen('junk1.dat', 'r');
a=fscanf(fp1, '%f');
fclose(fp1);

fp2=fopen('junk2.dat', 'w');
fprintf(fp2, 'This is the first line.\n');
fclose(fp2);


File translated from TEX by TTH, version 4.03.
On 09 Nov 2022, 14:39.