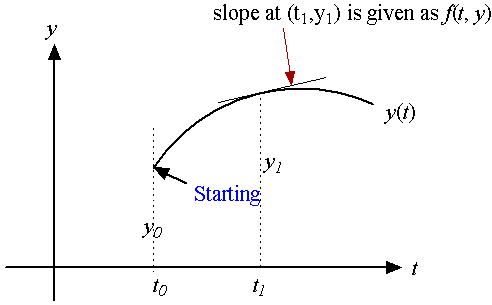
#21 (04/09/2025)

Statement of Differential Equations


dy
dt
 = f(t, y),
(1)
where t is the independent variable and f(t, y) is a function of t and y. Equation (1) along with the initial boundary condition of
y(t0) = y0,
(2)
is called the initial value problem.

Runge-Kutta method


k1
=
f(t, y)
k2
=
f(t + h
2
 , y + h
2
 k1)
k3
=
f(t + h
2
 , y + h
2
 k2)
k4
=
f(t + h, y + h k3),

yn+1 = yn + h k1 + 2 k2 + 2 k3 + k4
6
 .
(3)
#include <stdio.h>
#include <math.h>

double f(double t, double y)
 {
  return y;
 }

int main()
 {
  double h = 0.1, t, y, k1, k2, k3, k4;
  int i;

/* initial value */
  t = 0.0; y = 1.0;

 for (i = 0; i<=10; i++)
  {

   printf("t= %f rk= %f exact=%f\n", t, y, exp(t));
   k1 = h * f(t,y);
   k2 = h * f(t + h/2, y + k1/2.0);
   k3 = h * f(t + h/2, y + k2/2.0);
   k4 = h * f(t + h, y + k3);
   y = y + (k1 + 2.0 * k2 + 2.0 * k3 + k4)/6.0;
   t = t + h;
}
 return 0;
}

Higher order ODE

Example
d2 y
dt2
 = − y,     y(0)=0,     y′(0)=1.
(4)
By setting
y1 ≡ y,     y2 ≡ dy1
dt
 ,
the equation above is converted to

dy1
dt
=
y2
(5)
dy2
dt
=
−y1,
(6)
with
y1(0)=0,     y2(0)=1.
The exact solutions are y1=sin(t) and y2=cos(t). 
#include <stdio.h>
#include <math.h>

double f1(double t, double y1, double y2)
 {
  return y2;
 }

double f2(double t, double y1, double y2)
 {
  return -y1;
 }

int main()
 {
 double h = 0.02, y1, y2, t;
 int i;

 y1 = 0.0; y2 = 1.0;
 t = 0.0;

 for (i = 0; i<=100; i++)
  {
   printf("%f %f %f\n", t, y1, sin(t));
   y1 = y1 + h * f1(t, y1, y2);
   y2 = y2 + h * f2(t, y1, y2);
   t = t + h;
  }
 return 0;
}


Example (Lorenz equations/Strange Attracor/Chaos)

du
dt
=
p (v − u)
(7)
dv
dt
=
−u w + R u − v
(8)
dw
dt
=
u v − b w
(9)
#include <stdio.h>
#include <math.h>
#define P 16.0
#define b 4.0
#define R 35.0

double f1(double u, double v, double w)
 {
  return P*(v-u);
 }

double f2(double u, double v, double w)
 {
  return -u*w+R*u-v;
 }

double f3(double u, double v, double w)
 {
  return u*v-b*w;
 }

int main()
 {
  double h, t, u, v, w;
  int i;

  /* initial value */
  t = 0.0; h = 0.01;
  u = 5.0; v = 5.0; w = 5.0;

  for (i = 0; i< 3000; i++)
   {
    u = u + h * f1(u,v,w);
    v = v + h * f2(u,v,w);
    w = w + h * f3(u,v,w);
    printf("%f %f\n", u, w);
    t = t + h;
  }
 return 0;
 }

c:\tmp\gcc -o lorenz.exe lorenz.c
c:\tmp\lorenz.exe > lorenz.dat
(Launch gnuplot)
Change directory to c:\tmp
plot "lorenz.dat" with line
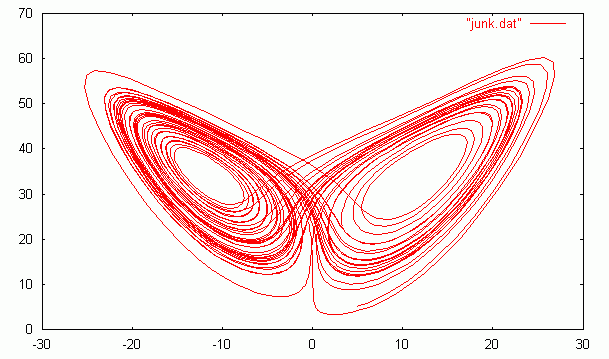Here is a code in Matlab/Octave. 
P=16;b=4;R=35;
f1=@(u,v,w) P*(v-u);
f2=@(u,v,w) -u*w+R*u-v;
f3=@(u,v,w) u*v-b*w;

t=0;h=0.01;
u=5;v=5;w=5;

for i=1:1:3000
 u=u+h*f1(u,v,w);
 v=v+h*f2(u,v,w);
 w=w+h*f3(u,v,w);
 uu(i)=u;vv(i)=v; 
 t=t+h;
end;

plot(uu',vv');

Matalb cheat for differential equations

The following code numerically solves the differential equation:

dy
dt
 = −t2 y,     y(0) = 1.
f=@(t,y) -t*t*y;
tspan=linspace(0,5,100);
y0=1;
[t,y]=ode45(f, tspan, y0);
plot(t,y);

Octave cheat for differential equations

The following code numerically solves the differential equation:

dy
dt
 = −t2 y,     y(0) = 1.
f=@(y,t) -t*t*y;
tspan=linspace(0, 3, 100);
y0=1;
sol=lsode(f, y0, tspan);
plot(tspan, sol);


File translated from TEX by TTH, version 4.03.
On 14 Apr 2025, 10:11.