#13 (07/21/2025)

Numerical differentiation

Analytical differentiation

First, some non-numerical (analytical) differentiation


f (x) f ′(x) Examples
(f ± g)′ f ′± g ′ (x + ex) ′
(f g) ′ f ′g + f g ′ (f g h) ′
(f/g) ′ (f ′g − f g ′)/g2 x/sin x
f (g (x)) ′ f ′(g (x)) g ′(x) (x2 + 1)10
xα αxα−1 x5, √x, √{x3}
ex ex ex2, 2x
ln x 1/x ln (x3)
sin x cos x sin (1+x2)
cos x −sin x cos (x2)
tan x 1/cos 2 x tan (x2+1)
arcsin x 1/√{1−x2} arcsin (arcsin (x))
arccos x −1/√{1−x2}
arctan x 1/(1+x2)

Some exercise:

    (a)
    (2x2 + 3)2 (3 x + 1)2

    (b)
    c x + d
    a x + b

    (c)

    √
     
    x2 − a2
     

    (d)
    1

    √
    a2 − x2

    (e)
    exp(−h2 x2)

    (f)
    cos2  3 x

    (g)
    ln (tan x)

    (h)
    tan−1   1 + x
    1 − x

Numerical differentiation

The only occasion where numerical differentiation is needed is when data are given numerically only, i.e.
x f (x)
1 1
2 8
3 27
4 64
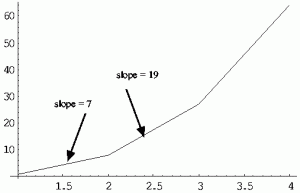
numdiff.gif

Forward difference


f (x + h)
=
f (x) + h f ′(x) + h2
2!
 f  " (x) + h3
3!
 f  "′(x)+…
(1)
≈
f (x) + h f ′(x),
(2)
hence
f ′(x) ≈ f (x + h) − f (x)
h
 .
(3)

Backward difference


f ( x − h )
=
f (x) − h f ′(x) + h2
2!
 f  "(x) − h3
3!
 f  "′(x) + …
≈
f (x) − h f ′(x),
(4)
hence
f ′(x) ≈ f (x) − f (x − h)
h
 .
(5)

Central difference


f (x + h)
=
f (x) + h f ′(x) + h2
2!
 f  "(x) + h3
3!
 f  "′(x)+…
(6)
f (x − h)
=
f (x) − h f ′(x) + h2
2!
 f  "(x) − h3
3!
 f  "′(x)+…
(7)
from which
f ( x + h ) − f ( x − h ) = 2 h f ′(x) + 2 h3
3!
 f  "′(x)+ …
(8)
hence

f ′(x) ≈ f ( x + h )− f ( x − h )
2h
 .
(9)
It is seen from the above that the central difference should yield better approximation as the truncation error is in the order of h2 while the truncation error for the forward and backward difference methods is in the order of h.

Second order derivative


f (x + h)
=
f (x)+h f ′(x) + h2
2!
 f  "(x) + h3
3!
 f  "′(x)+…
(10)
f (x − h)
=
f (x)−h f ′(x) + h2
2!
 f  "(x) − h3
3!
 f  "′(x)+…
(11)
Adding the above two yields

f (x + h)+f (x − h) = 2 f (x) + h2 f  "(x) + …
(12)
so

f  "(x) ≈ f (x + h) + f (x − h) − 2 f (x)
h2
 .
(13)

Example

The program below is to numerically differentiate a function given by the table below (numerical values of sin x for x = 0.0  ∼ 1.0). for x = 0 to x = 1 with the step size of h = 0.1 excluding at x=0 and x=1.0 where the central difference scheme does not work.
x 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
f(x) 00.09980.19860.29550.38940.47940.56460.64420.71730.78330.8414 


#include <stdio.h>
#define N 11

int main()
{
double y[N]={0, 0.0998, 0.1986, 0.2955, 0.3894, 0.4794, 0.5646, 0.6442, 0.7173, 0.7833, 0.8414};
double central[N], h=0.1;
int i;

/* Excluding x=0 and x=1.0 */
for (i=1;i<N-1;i++) central[i]= (y[i+1]-y[i-1])/(2*h);

printf ("   x    Central \n---------------------------\n");

for (i=1;i<N-1;i++)
 printf ("%lf %lf\n", i*h, central[i]);

return 0;
}

What if you want to obtain f′(x) at x = a with the same accuracy as the central difference ?

Obviously you cannot use the central difference scheme at x=a. Using the forward difference scheme, one can get

f′(x)  ∼  f(x+h) − f(x)
h
which is a poor approximation at best.
Consider

f(x + h)
=
f(x) + h f′(x) + h2
2!
 f"(x) + …
(14)
f(x + 2 h)
=
f(x) + 2 h f′(x) + 4 h2
2!
 f"(x) + …
(15)
The h2 term can be eliminated if one subtracts Eq.(15) from 4 times Eq.(14) as

4 f(x + h) − f(x + 2 h) = 3 f(x) + 2 h f′(x) + (higher order) …
(16)
from which one obtains

f′(x)  ∼  4 f(x+h) − f(x+2h) − 3 f(x)
2 h
(17)
Eq.(17) has the same order of accuracy as the central difference scheme.
So the program above can be modified as: 


#include <stdio.h>
#define N 11

int main()
{
double y[N]={0, 0.0998, 0.1986, 0.2955, 0.3894, 0.4794, 0.5646, 0.6442, 0.7173, 0.7833, 0.8414};
double central[N], h=0.1;
int i;

for (i=1;i<N-1;i++) central[i]= (y[i+1]-y[i-1])/(2*h);

central[0]=(4*y[1]-y[2]-3*y[0])/(2*h);

printf ("   x    Central \n---------------------------\n");

for (i=0;i<N-1;i++)
 printf ("%lf %lf\n", i*h, central[i]);

return 0;
}

Numerical Integration

Some of important integrals:


⌠
⌡ 		xα dx
xα+ 1
α+ 1
⌠
⌡ 		1
x
 dx
ln x
⌠
⌡ 		dx
1 + x2
arctan x
⌠
⌡ 		dx

√
a2 − x2
arcsin (x/a)
⌠
⌡ 		f(x) g′(x) dx
f(x)g(x) −⌠
⌡ 		f′(x) g(x) dx
⌠
⌡ 		f(x) dx
x f(x) − ⌠
⌡ 		x f′(x) dx

Exercises

Evaluate the following integrals:

(a) ⌠
⌡ 		dx
ex + e−x
(b)
⌠
⌡
√
 
a2 − x2
 
 dx
(c) ⌠
⌡ 		eax cos b x dx
(d)
⌠
⌡
√
 
x2 + 1
 
 dx
It is more practical these days to carry out integrations via computer.
Enter the following line 
Sqrt[x^2 + 1]
exactly (case sensitive, square bracket) in the first box and x (lower case) in the second box, then press the query button.
Integrate with respect to .

Numerical integrals:

numint.gif
  • Rectangular rule:

    I
     ∼ 
    h ×f0 + h ×f1 + h ×f2 + …+ h ×fn−1
    		(18)
    =
    h ( f0 + f1 + …+ fn−1 ).
    		(19)
    Sample program Implement
    4 ⌠
    ⌡     		1

    0 
    		 1
    1+x2
    		 dx = 4 arctan x⎢
    ⎢     		1
    0 
    		 = π.
    to approximate the value of π. 
    

    /* Rectangular rule */
#include <stdio.h>

double f(double x)
 {return 4.0/(1.0+x*x) ; }

int main()
{
 int i, n;
 double a=0.0, b=1.0, h, s=0.0 , x ;

 printf("Number of partitions = ");
 scanf("%d", &n) ;

 h = (b-a)/n ;

 for (i= 0;i<n;i++) s = s + f(a + i*h) ;

  s=s*h ;

  printf("Result =%lf\n", s) ;
  return 0;
}
  • Trapezoidal rule:
    trap.gif

    I
     ∼ 
    h
    2
    		 ( f0 + f1 ) + h
    2
    		 ( f1 + f2 )+ h
    2
    		 ( f2 + f3 )+ …+ h
    2
    		 ( fn−1 + fn )
    =
    h
    2
    		 (f0 + 2 f1 + 2f2 +…+2fn−1+fn).
    		(20)
    Implementation

    I  ∼  h
    2
    		 (f0+fn) + h ×(f1+f2+f3+…+ fn−1).
    /* Trapezoidal rule */
#include <stdio.h>

double f(double x)
 {return 4.0/(1.0+x*x);}

int main()
{
 int i, n ;
 double a=0.0, b=1.0 , h, s=0.0, x;

 printf("Enter number of partitions = ");
 scanf("%d", &n) ;

 h = (b-a)/n ;

 for (i=1;i<=n-1;i++) s = s + f(a + i*h);

  s=h/2*(f(a)+f(b))+ h* s;

  printf("%20.12f\n", s) ;
  return 0;
}
  • Simpson's rule:
    simpson.gif
    Approximate the curve that passes (−h, f(−h)), (0, f(0)) and (h, f(h)) by
    y = a x2+ b x + c.
    		(21)

    f(−h)
    =
    a h2 − b h + c,
    		(22)
    f(0)
    =
    c,
    		(23)
    f(h)
    =
    a h2+ b h + c,
    		(24)
    from which

    a
    =
    f(h)+ f(−h) − 2 f(0)
    2h2
    		 ,
    		(25)
    b
    =
    f(h)−f(−h)
    2h
    		 ,
    		(26)
    c
    =
    f(0).
    		(27)
    Hence,

    ⌠
    ⌡     		h

    −h 
    		 (a x2 + b x+ c) dx
    =
    ⌠
    ⌡     		h

    −h 
    		 ⎛
    ⎝     		f(h)+ f(−h) − 2 f(0)
    2h2
    		 x2 + f(h)−f(−h)
    2h
    		 x+ f(0)⎞
    ⎠     		dx
    =
    …
    =
    h
    3
    		 ⎛
    ⎝     		f(−h)+ 4 f(0)+ f(h)⎞
    ⎠     		.
    		(28)
    This is like a weighted average of f(−h), f(0) and f(h) as

    S ≈ f(−h)+ 4 f(0)+ f(h)
    6
    		 ×(2h).
    		(29)
    By adding this for the interval [a,b], one obtains

    I
     ∼ 
    h
    3
    		 ⎛
    ⎝     		(f0 + 4f1 + f2 )+(f2 + 4f3 + f4 )+(f4 + 4f5 + f6 )+…+(f2n−2+ 4 f2n−1+f2n )⎞
    ⎠
     ∼ 
    h
    3
    		 ⎛
    ⎝     		f0 +4 f1+2 f2 + 4f3 + 2f4 + …+ 2 f2n−2 + 4 f2n−1 + f2n⎞
    ⎠     		,
    		(30)
where
h = b−a
2n
 .
Note that the number of partitioning for the Simpson rule must be an even number (=2n).
For the coding purpose, it is convenient to write Eq.(30) as

I
=
h
3
 ⎛
⎝ 		f0+f2n⎞
⎠
+
h
3
 ×4 ⎛
⎝ 		f1 + f3 + f5 + …+f2n−1⎞
⎠
+
h
3
 ×2 ⎛
⎝ 		f2+f4+ f6 + …+ f2n−2⎞
⎠ 		.
(31)
Implementation 


/* Simpson's rule */
#include <stdio.h>
#include <math.h>

double f(double x)
 {return 4.0/(1.0+x*x);}

int main()
{
 int i, n ;
 double a=0.0, b=1.0 , h, s1=0.0, s2=0.0, s3=0.0, x;

 printf("Enter number of partitions  = ");
 scanf("%d", &n) ;

  h = (b-a)/(2.0*n) ;

  s1 = (f(a)+ f(b));

 for (i=1; i<2*n; i=i+2) s2 = s2 + f(a + i*h);

 for (i=2; i<2*n; i=i+2) s3 = s3 + f(a + i*h);

    printf("%20.12lf\n", (h/3.0)*(s1+ 4.0*s2 + 2.0*s3)) ;
 return 0;
}
According to error analysis, the truncation error for each rule is as follows:
  • Rectangular rule
    I  ∼ A + f′(ξ) h
  • Trapezoidal rule
    I  ∼ A + f"(ξ) h2
  • Simpson's rule
    I  ∼ A + f"′(ξ) h3
where h is the step size and ξ is a value within the interval.

Computation of π


⌠
⌡ 		1

0 
 1
1+x2
 dx = π
4
 .
1overx2plus1.gif

⌠
⌡ 		1

0 
√
 
1−x2
 
 dx = π
4
 .
sqrt1minusx2.gif
It is important to know that the accuracy of numerical integration generally depends on the derivatives of the function, f(x), to be integratated. Although the two examples above yield approximation to π, the convergence speed (and accuracy) varies greatly. For further information, read the following link:
 Error analysis


File translated from TEX by TTH, version 4.03.
On 20 Jul 2025, 17:52.