1. Algebraic equations
   According to the Galois theorem, it is not possible to solve general algebraic equations of the fifth order and beyond in closed form.
   1. Quadratic equations
      

      a x2 + b x + c = 0,     x = −b ± √ b2−4ac 2a .

      (1)

      Example:
      

      x2 + 200000 x − 3 = 0.

      (2)

      The exact solutions are
      

      x1 = −200000,     x2 = 0.000015,

      (3)

      #include <stdio.h> #include <math.h> int main() { float a, b, c, disc,x1, x2; a=1.0;b=200000;c=-3; disc=b*b-4*a*c; x1=(-b-sqrt(disc))/(2*a); x2=(-b+sqrt(disc))/(2*a); printf("x1 = %f, x2 = %f\n",x1,x2); return 0; }

      What went wrong ??
      From eq.(1), one obtains
      

      D = 200002 − 4×1.0 ×(−3) (4) = 40000000012, (5) √D = 200000.00003 (6)

      On the other hand,
      

      b = 200000.0 (7)

      Subtraction of two numbers with similar magnitude may result in cancellation error.
      Solution 1 Change float to double
      Solution 2 Noting that
      

      a x2 + b x +c = a(x−x1) (x−x2) (8) = a (x2 − (x1+x2) x + x1 x2) (9) = a x2 − a (x1+x2) x+ a x1 x2, (10)

      so
      
      

      x1 x2 = c a ,

      (11)

      hence
      

      x2 = c x1 a = −3 −200000 = 0.000015.

      (12)

      Solution 3 Rationalization:
      
      

      x2 = −b + √D 2a (13) = (−b−√D)(−b+√D) 2a (−b − √D) (14) = b2 − D 2a (−b − √D) , (15)

      so
      

      x2 = −2000002 − 40000000012 2 (−200000 − 200000) = 0.000015.

      (16)
   2. Cubic equations
      

      x3 + a x2 + b x+ c = 0.

      (17)

      (Try MathCheat.)
   3. Quartic equations
      

      x4 + a x3 + b x2+ c x + d = 0.

      (18)

      (Try MathCheat.)
2. Bisection method
   The mean value theorem:
   If f(x) is continuous over x₁ ≤ x ≤ x₂ and f′(x) exists over x₁ < x < x₂ and f(x₁) f(x₂) < 0, there is at least one point x between x₁ and x₂ such that f(x)=0.
   
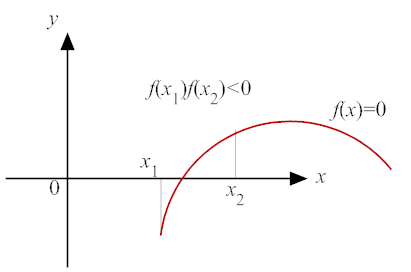
   1. Choose x₁ and x₂ such that f(x₁) f(x₂) < 0.
   2. Set x₃ ← (x₁+x₂)/2.
   3. If f(x₁) f(x₃) < 0, then, set x₂ ← x₃.
   4. Else set x₁ ← x₃.
   5. Until |x₁ − x₂| < ϵ or f(x₃) = 0, repeat b-d.
   

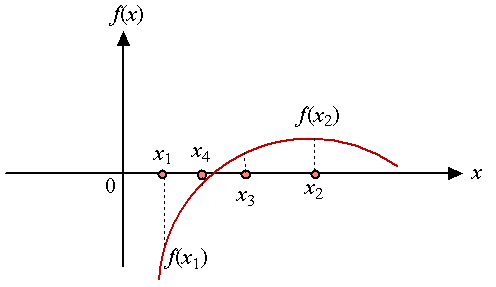
   /* Compute the square root of 2 */ #include <stdio.h> #include <math.h> #define EPS 1.0e-10 #define N 100 double f(double x) { return pow(x,2)-2; } /* start of main */ int main() { double x1, x2, x3; int count; printf("Enter xleft and xright separated by space ="); scanf("%lf %lf", &x1, &x2); /* sanity check */ if (f(x1)*f(x2)>0) {printf("Invalid x1 and x2 !\n"); return 0;} /* bisection start */ for (count=0;count< N; count++) { x3= (x1+x2)/2.0; if (f(x1)*f(x3)<0 ) x2=x3; else x1=x3; if ( f(x3)==0.0 || fabs(x1-x2)< EPS ) break; } printf("iteration = %d\n", count); printf("x= %lf\n", x1); return 0; }

   Notes:
   1. fabs is a function to return the absolute value of the argument in math.h (list of functions)
   2. Try plotting a graph by gnuplot first.
   Example: By solving e^x=2, obtain approximation of ln 2.
3. Newton-Raphson Method
   
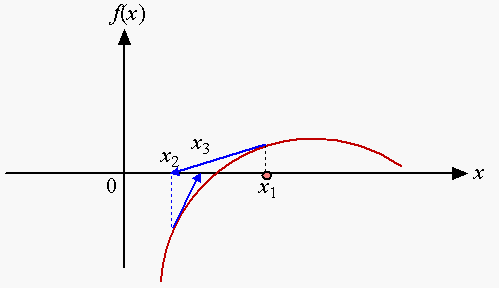   The equation of a straight line that passes (a,b) with a slope of m is
   

   y − b = m (x − a),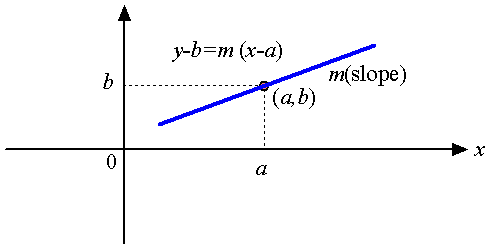

   
   so the tangent line that passes (x₁, f(x₁)) with the slope of f ′(x₁) is
   
   

   y − f(x1) = f ′(x1) (x−x1).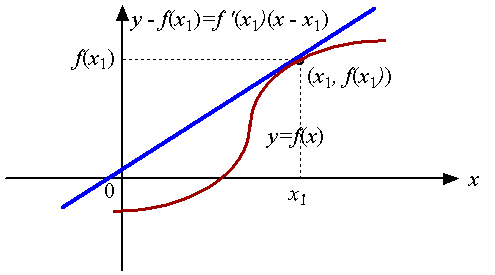

   
   
   

   0 − f(x1) = f ′(x1) (x−x1),

   
   

   x = x1 − f(x1) f ′(x1) ,

   
   

   x2 = x1 − f(x1) f ′(x1) .

   
   

   x3 = x2 − f(x2) f ′(x2) ,

   General forms:
   
   

   xn+1 = xn − f(xn) f ′(xn) .

   Example: √2
   By solving f(x) ≡ x² − 2 = 0 one can obtain a numerical value of √2.
   
   

   f(x) = x2 −2, f ′(x) = 2 x.

   (19)

   Start with x₁=2.0 (initial guess), then,
   

   x1 = 2 (20) x2 = 2− f(2) f ′(2) = 2 − 2 4 = 1.5 (21) x3 = 1.5 − f(1.5) f ′(1.5) = 1.5 − 0.25 3 = 1.41667 (22) x4 = 1.4167− f(1.4167) f ′(1.4167) = … = 1.4142. (23)

   The convergence is attained after only 4 iterations.
   Algorithm:
   1. Pick an initial guess, x₁.
   2. Make sure f ′(x₁) ≠ 0.
   3. Repeat
      1. x₂ ← x₁ − f(x₁)/f ′(x₁)
      2. x₁ ← x₂
   4. Until |x₁−x₂| ≤ ϵ.
   The Newton-Raphson method fails when f ′(x_n) is zero.

   #include <stdio.h> #include <math.h> #define EPS 1.0e-10 double f(double x) { return x*x-2; } double fp(double x) { return 2*x; } double newton(double x) { return x - f(x)/fp(x); } int main() { double x1, x2; int i; printf("Enter initial guess  ="); scanf("%lf", &x1); if (fp(x1)==0.0) { printf("No convergence.\n"); return 0; } for (i=0;i<100;i++) { x2=newton(x1); if (fabs(x1-x2)< EPS) break; x1=x2; } printf("iteration = %d\n", i); printf("x= %lf\n", x1); return 0; }

   Some interesting examples

   The following examples are useful in emergency when you do not have an access to a computer.
   1. Square root of a ( = √a)
      Let f(x) = x² − a, the Newton-Raphson method yields
      
      

      xn+1 = xn − xn2 − a 2 xn (24) = 1 2 ⎛ ⎝ xn + a xn ⎞ ⎠ . (25)

      Example (√3 = 1.732 …)
      

      x1=1,     x2 = 1 2 (1 + 3 1 ) = 2,    x3 = 1 2 (2 + 3 2 ) = 1.75,    x4 = 1 2 (1.75 + 3 1.75 ) = 1.732.
   2. Inverse of a ( = 1/a)
      Let f(x) = 1/x − a, the Newton-Raphson method yields
      

      xn+1 = xn − 1 xn −a −1 xn2 (26) = xn (2 − a xn). (27)

      In case you forgot how to do divisions, you can use this formula.
      Example (1/6 = 0.16667…)
      
      

      x1 = 0.2,     x2 = 0.2 (2 − 6×0.2)=0.16,    x3 = 0.16 (2 − 6×0.16) = 0.1664,    x4 = 0.1664 (2 − 6×0.1664) = 0.166666.
   3. 1/√a
      Let f(x) = 1/x² − a,
      
      

      xn+1 = xn − 1/xn2 − a − 2/xn3 (28) = xn (3 − a xn2)/2. (29)

Summary

• Bisection method
  • Convergence guaranteed
  • Slow
  • Needs two initial points
• Newton-Raphson method
  • Convergence not guaranteed
  • Super fast
  • Needs one initial point

Solving simultaneous equations

Determinant

1. 2 ×2 matrices
   

   ⎢ ⎢ ⎢ ⎢ a11 a12 a21 a22. ⎢ ⎢ ⎢ ⎢ ≡ a11 a22− a12 a21

   (33)
2. 3 ×3 matrices
   

   ⎢ ⎢ ⎢ ⎢ ⎢ a11 a12 a13 a21 a22 a23 a31 a32 a33 ⎢ ⎢ ⎢ ⎢ ⎢ ≡ a11 a22 a33 + a12 a23 a31+ a21 a32 a13− a13 a22a31−a12 a21 a33 − a23 a32 a11

   (34)
3. The determinant of n ×n (n > 3) matrices can be expressed similar to the above. It consists of n! terms each of which is a product of n variables.

Some properties of determinants

1. | A B | = | A | | B |
2. | I | = 1 where I is the identity matrix.
3. | A |=0 ⇒ A is singular.

Determinant/Cramer's rule